PROBLEM 1.1
A spacecraft's engine ejects mass at a rate of 30 kg/s with an exhaust velocity
of 3,100 m/s. The pressure at the nozzle exit is 5 kPa and the exit area is
0.7 m2. What is the thrust of the engine in a vacuum?
SOLUTION,
Given: q = 30 kg/s
Ve = 3,100 m/s
Ae = 0.7 m2
Pe = 5 kPa = 5,000 N/m2
Pa = 0
Equation (1.6),
F = q × Ve + (Pe - Pa) × Ae
F = 30 × 3,100 + (5,000 - 0) × 0.7
F = 96,500 N
PROBLEM 1.2
The spacecraft in problem 1.1 has an initial mass of 30,000 kg. What is the
change in velocity if the spacecraft burns its engine for one minute?
SOLUTION,
Given: M = 30,000 kg
q = 30 kg/s
Ve = 3,100 m/s
t = 60 s
Equation (1.16),
 V = Ve × LN[ M / (M - qt) ]
V = Ve × LN[ M / (M - qt) ]
 V = 3,100 × LN[ 30,000 / (30,000 - (30 × 60)) ]
V = 3,100 × LN[ 30,000 / (30,000 - (30 × 60)) ]
 V = 192 m/s
V = 192 m/s
PROBLEM 1.3
A spacecraft's dry mass is 75,000 kg and the effective exhaust gas velocity
of its main engine is 3,100 m/s. How much propellant must be carried if the
propulsion system is to produce a total  v of 700 m/s?
SOLUTION,
Given: Mf = 75,000 kg
C = 3,100 m/s
v of 700 m/s?
SOLUTION,
Given: Mf = 75,000 kg
C = 3,100 m/s
 V = 700 m/s
Equation (1.20),
Mo = Mf × e(DV / C)
Mo = 75,000 × e(700 / 3,100)
Mo = 94,000 kg
Propellant mass,
Mp = Mo - Mf
Mp = 94,000 - 75,000
Mp = 19,000 kg
V = 700 m/s
Equation (1.20),
Mo = Mf × e(DV / C)
Mo = 75,000 × e(700 / 3,100)
Mo = 94,000 kg
Propellant mass,
Mp = Mo - Mf
Mp = 94,000 - 75,000
Mp = 19,000 kg
PROBLEM 1.4
A 5,000 kg spacecraft is in Earth orbit traveling at a velocity of 7,790 m/s.
Its engine is burned to accelerate it to a velocity of 12,000 m/s placing it
on an escape trajectory. The engine expels mass at a rate of 10 kg/s and an
effective velocity of 3,000 m/s. Calculate the duration of the burn.
SOLUTION,
Given: M = 5,000 kg
q = 10 kg/s
C = 3,000 m/s
 V = 12,000 - 7,790 = 4,210 m/s
Equation (1.21),
t = M / q × [ 1 - 1 / e(DV / C) ]
t = 5,000 / 10 × [ 1 - 1 / e(4,210 / 3,000) ]
t = 377 s
V = 12,000 - 7,790 = 4,210 m/s
Equation (1.21),
t = M / q × [ 1 - 1 / e(DV / C) ]
t = 5,000 / 10 × [ 1 - 1 / e(4,210 / 3,000) ]
t = 377 s
PROBLEM 1.5
A rocket engine burning liquid oxygen and kerosene operates at a mixture ratio
of 2.26 and a combustion chamber pressure of 50 atmospheres. If the nozzle is
expanded to operate at sea level, calculate the exhaust gas velocity relative
to the rocket.
SOLUTION,
Given: O/F = 2.26
Pc = 50 atm
Pe = Pa = 1 atm
From LOX/Kerosene Charts we estimate,
Tc = 3,470 K
M = 21.40
k = 1.221
Equation (1.22),
Ve = SQRT[ (2 × k / (k - 1)) × (R* × Tc / M) × (1 - (Pe / Pc)(k-1)/k) ]
Ve = SQRT[ (2 × 1.221 / (1.221 - 1)) × (8,314.46 × 3,470 / 21.40) × (1 - (1 / 50)(1.221-1)/1.221) ]
Ve = 2,749 m/s
PROBLEM 1.6
A rocket engine produces a thrust of 1,000 kN at sea level with a propellant
flow rate of 400 kg/s. Calculate the specific impulse.
SOLUTION,
Given: F = 1,000,000 N
q = 400 kg/s
Equation (1.23),
Isp = F / (q × g)
Isp = 1,000,000 / (400 × 9.80665)
Isp = 255 s (sea level)
PROBLEM 1.7
A rocket engine uses the same propellant, mixture ratio, and combustion chamber
pressure as that in problem 1.5. If the propellant flow rate is 500 kg/s,
calculate the area of the exhaust nozzle throat.
SOLUTION,
Given: Pc = 50 × 0.101325 = 5.066 MPa
Tc = 3,470<sup.o< sup=""> K
M = 21.40
k = 1.221
q = 500 kg/s
Equation (1.27),
Pt = Pc × [1 + (k - 1) / 2]-k/(k-1)
Pt = 5.066 × [1 + (1.221 - 1) / 2]-1.221/(1.221-1)
Pt = 2.839 MPa = 2.839×106 N/m2
Equation (1.28),
Tt = Tc / (1 + (k - 1) / 2)
Tt = 3,470 / (1 + (1.221 - 1) / 2)
Tt = 3,125 K
Equation (1.26),
At = (q / Pt) × SQRT[ (R* × Tt) / (M × k) ]
At = (500 / 2.839×106) × SQRT[ (8,314.46 × 3,125) / (21.40 × 1.221) ]
At = 0.1756 m2
</sup.o<>
PROBLEM 1.8
The rocket engine in problem 1.7 is optimized to operate at an elevation of 2000
meters. Calculate the area of the nozzle exit and the section ratio.
SOLUTION,
Given: Pc = 5.066 MPa
At = 0.1756 m2
k = 1.221
From Atmosphere Properties,
Pa = 0.0795 MPa
Equation (1.29),
Nm2 = (2 / (k - 1)) × [(Pc / Pa)(k-1)/k - 1]
Nm2 = (2 / (1.221 - 1)) × [(5.066 / 0.0795)(1.221-1)/1.221 - 1]
Nm2 = 10.15
Nm = (10.15)1/2 = 3.185
Equation (1.30),
Ae = (At / Nm) × [(1 + (k - 1) / 2 × Nm2)/((k + 1) / 2)](k+1)/(2(k-1))
Ae = (0.1756 / 3.185) × [(1 + (1.221 - 1) / 2 × 10.15)/((1.221 + 1) / 2)](1.221+1)/(2(1.221-1))
Ae = 1.426 m2
Section Ratio,
Ae / At = 1.426 / 0.1756 = 8.12
PROBLEM 1.9
For the rocket engine in problem 1.7, calculate the volume and dimensions of a
possible combustion chamber. The convergent cone half-angle is 20 degrees.
SOLUTION,
Given: At = 0.1756 m2 = 1,756 cm2
Dt = 2 × (1,756/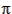 )1/2 = 47.3 cm
)1/2 = 47.3 cm
 = 20o
From Table 1,
L* = 102-127 cm for LOX/RP-1, let's use 110 cm
Equation (1.33),
Vc = At × L*
Vc = 1,756 × 110 = 193,160 cm3
From Figure 1.7,
Lc = 66 cm (second-order approximation)
Equation (1.35),
Dc = SQRT[(Dt3 + 24/
= 20o
From Table 1,
L* = 102-127 cm for LOX/RP-1, let's use 110 cm
Equation (1.33),
Vc = At × L*
Vc = 1,756 × 110 = 193,160 cm3
From Figure 1.7,
Lc = 66 cm (second-order approximation)
Equation (1.35),
Dc = SQRT[(Dt3 + 24/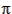 × tan
× tan  × Vc) / (Dc + 6 × tan
× Vc) / (Dc + 6 × tan  × Lc)]
Dc = SQRT[(47.33 + 24/
× Lc)]
Dc = SQRT[(47.33 + 24/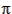 × tan(20) × 193,160) / (Dc + 6 × tan(20) × 66)]
Dc = 56.6 cm (four interations)
× tan(20) × 193,160) / (Dc + 6 × tan(20) × 66)]
Dc = 56.6 cm (four interations)
PROBLEM 1.10
A solid rocket motor burns along the face of a central cylindrical channel 10
meters long and 1 meter in diameter. The propellant has a burn rate coefficient
of 5.5, a pressure exponent of 0.4, and a density of 1.70 g/ml. Calculate the
burn rate and the product generation rate when the chamber pressure is 5.0 MPa.
SOLUTION,
Given: a = 5.5
n = 0.4
Pc = 5.0 MPa
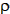 p = 1.70 g/ml
Ab =
p = 1.70 g/ml
Ab = 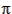 × 1 × 10 = 31.416 m2
Equation (1.36),
r = a × Pcn
r = 5.5 × 5.00.4 = 10.47 mm/s
Equation (1.37),
q =
× 1 × 10 = 31.416 m2
Equation (1.36),
r = a × Pcn
r = 5.5 × 5.00.4 = 10.47 mm/s
Equation (1.37),
q = 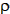 p × Ab × r
q = 1.70 × 31.416 × 10.47 = 559 kg/s
p × Ab × r
q = 1.70 × 31.416 × 10.47 = 559 kg/s
PROBLEM 1.11
Calculate the ideal density of a solid rocket propellant consisting of 68%
ammonium perchlorate, 18% aluminum, and 14% HTPB by mass.
SOLUTION,
Given: wAP = 0.68
wAl = 0.18
wHTPB = 0.14
From Properties of Rocket Propellants we have,
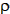 AP = 1.95 g/ml
AP = 1.95 g/ml
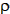 Al = 2.70 g/ml
Al = 2.70 g/ml
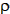 HTPB = ≈0.93 g/ml
Equation (1.38),
HTPB = ≈0.93 g/ml
Equation (1.38),
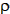 p = 1 /
p = 1 / 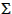 i (w /
i (w / 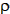 )i
)i
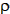 p = 1 / [(0.68 / 1.95) + (0.18 / 2.70) + (0.14 / 0.93)]
p = 1 / [(0.68 / 1.95) + (0.18 / 2.70) + (0.14 / 0.93)]
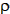 p = 1.767
p = 1.767
PROBLEM 1.12
A two-stage rocket has the following masses: 1st-stage propellant mass 120,000
kg, 1st-stage dry mass 9,000 kg, 2nd-stage propellant mass 30,000 kg, 2nd-stage
dry mass 3,000 kg, and payload mass 3,000 kg. The specific impulses of the
1st and 2nd stages are 260 s and 320 s respectively. Calculate the rocket's
total  V.
SOLUTION,
Given: Mo1 = 120,000 + 9,000 + 30,000 + 3,000 + 3,000 = 165,000 kg
Mf1 = 9,000 + 30,000 + 3,000 + 3,000 = 45,000 kg
Isp1 = 260 s
Mo2 = 30,000 + 3,000 + 3,000 = 36,000 kg
Mf2 = 3,000 + 3,000 = 6,000 kg
Isp2 = 320 s
Equation (1.24),
C1 = Isp1g
C1 = 260 × 9.80665 = 2,550 m/s
C2 = Isp2g
C2 = 320 × 9.80665 = 3,138 m/s
Equation (1.39),
V.
SOLUTION,
Given: Mo1 = 120,000 + 9,000 + 30,000 + 3,000 + 3,000 = 165,000 kg
Mf1 = 9,000 + 30,000 + 3,000 + 3,000 = 45,000 kg
Isp1 = 260 s
Mo2 = 30,000 + 3,000 + 3,000 = 36,000 kg
Mf2 = 3,000 + 3,000 = 6,000 kg
Isp2 = 320 s
Equation (1.24),
C1 = Isp1g
C1 = 260 × 9.80665 = 2,550 m/s
C2 = Isp2g
C2 = 320 × 9.80665 = 3,138 m/s
Equation (1.39),
 V1 = C1 × LN[ Mo1 / Mf1 ]
V1 = C1 × LN[ Mo1 / Mf1 ]
 V1 = 2,550 × LN[ 165,000 / 45,000 ]
V1 = 2,550 × LN[ 165,000 / 45,000 ]
 V1 = 3,313 m/s
V1 = 3,313 m/s
 V2 = C2 × LN[ Mo2 / Mf2 ]
V2 = C2 × LN[ Mo2 / Mf2 ]
 V2 = 3,138 × LN[ 36,000 / 6,000 ]
V2 = 3,138 × LN[ 36,000 / 6,000 ]
 V2 = 5,623 m/s
Equation (1.40),
V2 = 5,623 m/s
Equation (1.40),
 VTotal =
VTotal =  V1 +
V1 +  V2
V2
 VTotal = 3,313 + 5,623
VTotal = 3,313 + 5,623
 VTotal = 8,936 m/s
VTotal = 8,936 m/s
PROBLEM 3.1
Using the Barrowman method, calculate the location of the center of pressure from the
leading edge of a rocket having the dimensions given below. The nose is ogive shaped.
SOLUTION,
Given: LN = 400 mm
d = 200 mm
dF = 200 mm
dR = 160 mm
LT = 120 mm
XP = 900 mm
CR = 240 mm
CT = 120 mm
S = 240 mm
LF = 247 mm
R = 80 mm
XR = 120 mm
XB = 1,760 mm
N = 3 each
Equations (3.1) through (3.6),
(CN)N = 2
XN = 0.466 × LN
XN = 0.466 × 400 = 186 mm
(CN)T = 2 × [(dR / d)2 - (dF / d)2]
(CN)T = 2 × [(160 / 200)2 - (200 / 200)2]
(CN)T = -0.72
XT = XP + LT / 3 × [1 + (1 - dF / dR) / (1 - (dF / dR)2)]
XT = 900 + 120 / 3 × [1 + (1 - 200 / 160) / (1 - (200 / 160)2)]
XT = 958 mm
(CN)F = (1 + R / (S + R)) × [4 × N × (S / d)2 / (1 + SQRT[1 + (2 × LF / (CR + CT))2])]
(CN)F = (1 + 80 / (240 + 80)) × [4 × 3 × (240 / 200)2 / (1 + SQRT[1 + (2 × 247 / (240 + 120))2])]
(CN)F = 8.01
XF = XB + XR / 3 × (CR + 2 × CT) / (CR + CT) + 1/6 × [CR + CT - CR × CT / (CR + CT)]
XF = 1760 + 120 / 3 × (240 + 2 × 120) / (240 + 120) + 1/6 × [240 + 120 - 240 × 120 / (240 + 120)]
XF = 1,860 mm
Equations (3.7) and (3.8),
(CN)R = (CN)N + (CN)T + (CN)F
(CN)R = 2 - 0.72 + 8.01 = 9.29
X = [(CN)N × XN + (CN)T × XT + (CN)F × XF] / (CN)R
X = [2 × 186 - 0.72 × 958 + 8.01 × 1860] / 9.29
X = 1,570 mm
PROBLEM 4.1
Calculate the velocity of an artificial satellite orbiting the Earth in a
circular orbit at an altitude of 200 km above the Earth's surface.
SOLUTION,
From Basics Constants,
Radius of Earth = 6,378.14 km
GM of Earth = 3.986005×1014 m3/s2
Given: r = (6,378.14 + 200) × 1,000 = 6,578,140 m
Equation (4.6),
v = SQRT[ GM / r ]
v = SQRT[ 3.986005×1014 / 6,578,140 ]
v = 7,784 m/s
PROBLEM 4.2
Calculate the period of revolution for the satellite in problem 4.1.
SOLUTION,
Given: r = 6,578,140 m
Equation (4.9),
P2 = 4 × 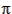 2 × r3 / GM
P = SQRT[ 4 ×
2 × r3 / GM
P = SQRT[ 4 × 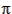 2 × r3 / GM ]
P = SQRT[ 4 ×
2 × r3 / GM ]
P = SQRT[ 4 × 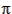 2 × 6,578,1403 / 3.986005×1014 ]
P = 5,310 s
2 × 6,578,1403 / 3.986005×1014 ]
P = 5,310 s
PROBLEM 4.3
Calculate the radius of orbit for a Earth satellite in a geosynchronous orbit,
where the Earth's rotational period is 86,164.1 seconds.
SOLUTION,
Given: P = 86,164.1 s
Equation (4.9),
P2 = 4 × 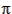 2 × r3 / GM
r = [ P2 × GM / (4 ×
2 × r3 / GM
r = [ P2 × GM / (4 × 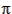 2) ]1/3
r = [ 86,164.12 × 3.986005×1014 / (4 ×
2) ]1/3
r = [ 86,164.12 × 3.986005×1014 / (4 × 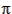 2) ]1/3
r = 42,164,170 m
2) ]1/3
r = 42,164,170 m
PROBLEM 4.4
An artificial Earth satellite is in an elliptical orbit which brings it to
an altitude of 250 km at perigee and out to an altitude of 500 km at apogee.
Calculate the velocity of the satellite at both perigee and apogee.
SOLUTION,
Given: Rp = (6,378.14 + 250) × 1,000 = 6,628,140 m
Ra = (6,378.14 + 500) × 1,000 = 6,878,140 m
Equations (4.16) and (4.17),
Vp = SQRT[ 2 × GM × Ra / (Rp × (Ra + Rp)) ]
Vp = SQRT[ 2 × 3.986005×1014 × 6,878,140 / (6,628,140 × (6,878,140 + 6,628,140)) ]
Vp = 7,826 m/s
Va = SQRT[ 2 × GM × Rp / (Ra × (Ra + Rp)) ]
Va = SQRT[ 2 × 3.986005×1014 × 6,628,140 / (6,878,140 × (6,878,140 + 6,628,140)) ]
Va = 7,542 m/s
PROBLEM 4.5
A satellite in Earth orbit passes through its perigee point at an altitude of
200 km above the Earth's surface and at a velocity of 7,850 m/s. Calculate the
apogee altitude of the satellite.
SOLUTION,
Given: Rp = (6,378.14 + 200) × 1,000 = 6,578,140 m
Vp = 7,850 m/s
Equation (4.18),
Ra = Rp / [2 × GM / (Rp × Vp2) - 1]
Ra = 6,578,140 / [2 × 3.986005×1014 / (6,578,140 × 7,8502) - 1]
Ra = 6,805,140 m
Altitude @ apogee = 6,805,140 / 1,000 - 6,378.14 = 427.0 km
PROBLEM 4.6
Calculate the eccentricity of the orbit for the satellite in problem 4.5.
SOLUTION,
Given: Rp = 6,578,140 m
Vp = 7,850 m/s
Equation (4.20),
e = Rp × Vp2 / GM - 1
e = 6,578,140 × 7,8502 / 3.986005×1014 - 1
e = 0.01696
PROBLEM 4.7
A satellite in Earth orbit has a semi-major axis of 6,700 km and an eccentricity
of 0.01. Calculate the satellite's altitude at both perigee and apogee.
SOLUTION,
Given: a = 6,700 km
e = 0.01
Equation (4.21) and (4.22),
Rp = a × (1 - e)
Rp = 6,700 × (1 - .01)
Rp = 6,633 km
Altitude @ perigee = 6,633 - 6,378.14 = 254.9 km
Ra = a × (1 + e)
Ra = 6,700 × (1 + .01)
Ra = 6,767 km
Altitude @ apogee = 6,767 - 6,378.14 = 388.9 km
PROBLEM 4.8
A satellite is launched into Earth orbit where its launch vehicle burns out at
an altitude of 250 km. At burnout the satellite's velocity is 7,900 m/s with the
zenith angle equal to 89 degrees. Calculate the satellite's altitude at perigee
and apogee.
SOLUTION,
Given: r1 = (6,378.14 + 250) × 1,000 = 6,628,140 m
v1 = 7,900 m/s
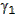 = 89o
Equation (4.26),
(Rp / r1)1,2 = ( -C ± SQRT[ C2 - 4 × (1 - C) × -sin2
= 89o
Equation (4.26),
(Rp / r1)1,2 = ( -C ± SQRT[ C2 - 4 × (1 - C) × -sin2 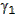 ]) / (2 × (1 - C))
where C = 2 × GM / (r1 × v12)
C = 2 × 3.986005×1014 / (6,628,140 × 7,9002)
C = 1.927179
(Rp / r1)1,2 = ( -1.927179 ± SQRT[ 1.9271792 - 4 × -0.927179 × -sin2(89) ]) / (2 × -0.927179)
(Rp / r1)1,2 = 0.996019 and 1.082521
Perigee Radius, Rp = Rp1 = r1 × (Rp / r1)1
Rp = 6,628,140 × 0.996019
Rp = 6,601,750 m
Altitude @ perigee = 6,601,750 / 1,000 - 6,378.14 = 223.6 km
Apogee Radius, Ra = Rp2 = r1 × (Rp / r1)2
Ra = 6,628,140 × 1.082521
Ra = 7,175,100 m
Altitude @ agogee = 7,175,100 / 1,000 - 6,378.14 = 797.0 km
]) / (2 × (1 - C))
where C = 2 × GM / (r1 × v12)
C = 2 × 3.986005×1014 / (6,628,140 × 7,9002)
C = 1.927179
(Rp / r1)1,2 = ( -1.927179 ± SQRT[ 1.9271792 - 4 × -0.927179 × -sin2(89) ]) / (2 × -0.927179)
(Rp / r1)1,2 = 0.996019 and 1.082521
Perigee Radius, Rp = Rp1 = r1 × (Rp / r1)1
Rp = 6,628,140 × 0.996019
Rp = 6,601,750 m
Altitude @ perigee = 6,601,750 / 1,000 - 6,378.14 = 223.6 km
Apogee Radius, Ra = Rp2 = r1 × (Rp / r1)2
Ra = 6,628,140 × 1.082521
Ra = 7,175,100 m
Altitude @ agogee = 7,175,100 / 1,000 - 6,378.14 = 797.0 km
PROBLEM 4.9
Calculate the eccentricity of the orbit for the satellite in problem 4.8.
SOLUTION,
Given: r1 = 6,628,140 m
v1 = 7,900 m/s
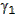 = 89o
Equation (4.27),
e = SQRT[ (r1 × v12 / GM - 1)2 × sin2
= 89o
Equation (4.27),
e = SQRT[ (r1 × v12 / GM - 1)2 × sin2 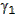 + cos2
+ cos2 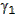 ]
e = SQRT[ (6,628,140 × 7,9002 / 3.986005×1014 - 1)2 × sin2(89) + cos2(89) ]
e = 0.0416170
]
e = SQRT[ (6,628,140 × 7,9002 / 3.986005×1014 - 1)2 × sin2(89) + cos2(89) ]
e = 0.0416170
PROBLEM 4.10
Calculate the angle  from perigee point to launch point for the satellite
in problem 4.8.
SOLUTION,
Given: r1 = 6,628,140 m
v1 = 7,900 m/s
from perigee point to launch point for the satellite
in problem 4.8.
SOLUTION,
Given: r1 = 6,628,140 m
v1 = 7,900 m/s
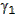 = 89o
Equation (4.28),
tan
= 89o
Equation (4.28),
tan  = (r1 × v12 / GM) × sin
= (r1 × v12 / GM) × sin 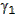 × cos
× cos 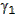 / [(r1 × v12 / GM) × sin2
/ [(r1 × v12 / GM) × sin2 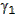 - 1]
tan
- 1]
tan  = (6,628,140 × 7,9002 / 3.986005×1014) × sin(89) × cos(89)
/ [(6,628,140 × 7,9002 / 3.986005×1014) × sin2(89) - 1]
tan
= (6,628,140 × 7,9002 / 3.986005×1014) × sin(89) × cos(89)
/ [(6,628,140 × 7,9002 / 3.986005×1014) × sin2(89) - 1]
tan  = 0.48329
= 0.48329
 = arctan(0.48329)
= arctan(0.48329)
 = 25.794o
= 25.794o
PROBLEM 4.11
Calculate the semi-major axis of the orbit for the satellite in problem 4.8.
SOLUTION,
Given: r1 = 6,628,140 m
v1 = 7,900 m/s
Equation (4.32),
a = 1 / ( 2 / r1 - v12 / GM )
a = 1 / ( 2 / 6,628,140 - 7,9002 / 3.986005×1014) )
a = 6,888,430 m
PROBLEM 4.12
For the satellite in problem 4.8, burnout occurs 2000-10-20, 15:00 UT. The
geocentric coordinates at burnout are 32o N latitude, 60o W longitude, and the
azimuth heading is 86o. Calculate the orbit's inclination, argument of perigee,
and longitude of ascending node.
SOLUTION,
Given: 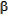 = 86o
= 86o
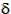 = 32o
= 32o
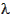 2 = -60o
From problem 4.10,
2 = -60o
From problem 4.10,
 = 25.794o
Equation (4.33),
cos(i) = cos(
= 25.794o
Equation (4.33),
cos(i) = cos(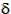 ) × sin(
) × sin(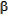 )
cos(i) = cos(32) × sin(86)
i = 32.223o
Equations (4.34) and (4.36),
tan(
)
cos(i) = cos(32) × sin(86)
i = 32.223o
Equations (4.34) and (4.36),
tan(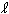 ) = tan(
) = tan(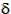 ) / cos(
) / cos(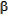 )
tan(
)
tan(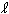 ) = tan(32) / cos(86)
) = tan(32) / cos(86)
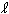 = 83.630o
= 83.630o
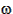 =
= 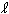 -
- 
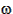 = 83.630 - 25.794
= 83.630 - 25.794
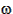 = 57.836o
Equations (4.35) and (4.37),
tan(
= 57.836o
Equations (4.35) and (4.37),
tan(
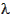 ) = sin(
) = sin(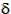 ) × tan(
) × tan(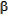 )
tan(
)
tan(
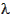 ) = sin(32) × tan(86)
) = sin(32) × tan(86)

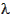 = 82.483o
= 82.483o
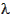 1 =
1 = 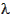 2 -
2 - 
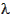
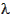 1 = -60 - 82.483
1 = -60 - 82.483
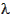 1 = -142.483o
1 = -142.483o
 = Sidereal time at -142.483 longitude, 2000-10-20, 15:00 UT
= Sidereal time at -142.483 longitude, 2000-10-20, 15:00 UT
 = 7h 27' 34" = 111.892o
= 7h 27' 34" = 111.892o
PROBLEM 4.13
A satellite is in an orbit with a semi-major axis of 7,500 km and an eccentricity
of 0.1. Calculate the time it takes to move from a position 30 degrees past
perigee to 90 degrees past perigee.
SOLUTION,
Given: a = 7,500 × 1,000 = 7,500,000 m
e = 0.1
tO = 0
 O = 30 deg ×
O = 30 deg × 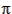 /180 = 0.52360 radians
/180 = 0.52360 radians
 = 90 deg ×
= 90 deg × 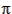 /180 = 1.57080 radians
Equation (4.40),
cos E = (e + cos
/180 = 1.57080 radians
Equation (4.40),
cos E = (e + cos  ) / (1 + e cos
) / (1 + e cos  )
Eo = arccos[(0.1 + cos(0.52360)) / (1 + 0.1 × cos(0.52360))]
Eo = 0.47557 radians
E = arccos[(0.1 + cos(1.57080)) / (1 + 0.1 × cos(1.57080))]
E = 1.47063 radians
Equation (4.41),
M = E - e × sin E
Mo = 0.47557 - 0.1 × sin(0.47557)
Mo = 0.42978 radians
M = 1.47063 - 0.1 × sin(1.47063)
M = 1.37113 radians
Equation (4.39),
n = SQRT[ GM / a3 ]
n = SQRT[ 3.986005×1014 / 7,500,0003 ]
n = 0.00097202 rad/s
Equation (4.38),
M - Mo = n × (t - tO)
t = tO + (M - Mo) / n
t = 0 + (1.37113 - 0.42978) / 0.00097202
t = 968.4 s
)
Eo = arccos[(0.1 + cos(0.52360)) / (1 + 0.1 × cos(0.52360))]
Eo = 0.47557 radians
E = arccos[(0.1 + cos(1.57080)) / (1 + 0.1 × cos(1.57080))]
E = 1.47063 radians
Equation (4.41),
M = E - e × sin E
Mo = 0.47557 - 0.1 × sin(0.47557)
Mo = 0.42978 radians
M = 1.47063 - 0.1 × sin(1.47063)
M = 1.37113 radians
Equation (4.39),
n = SQRT[ GM / a3 ]
n = SQRT[ 3.986005×1014 / 7,500,0003 ]
n = 0.00097202 rad/s
Equation (4.38),
M - Mo = n × (t - tO)
t = tO + (M - Mo) / n
t = 0 + (1.37113 - 0.42978) / 0.00097202
t = 968.4 s
PROBLEM 4.14
The satellite in problem 4.13 has a true anomaly of 90 degrees. What will be the
satellite's position, i.e. it's true anomaly, 20 minutes later?
SOLUTION,
Given: a = 7,500,000 m
e = 0.1
tO = 0
t = 20 × 60 = 1,200 s
 O = 90 ×
O = 90 × 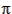 /180 = 1.57080 rad
From problem 4.13,
Mo = 1.37113 rad
n = 0.00097202 rad/s
Equation (4.38),
M - Mo = n × (t - tO)
M = Mo + n × (t - tO)
M = 1.37113 + 0.00097202 × (1,200 - 0)
M = 2.53755
METHOD #1, Low Accuracy:
Equation (4.42),
/180 = 1.57080 rad
From problem 4.13,
Mo = 1.37113 rad
n = 0.00097202 rad/s
Equation (4.38),
M - Mo = n × (t - tO)
M = Mo + n × (t - tO)
M = 1.37113 + 0.00097202 × (1,200 - 0)
M = 2.53755
METHOD #1, Low Accuracy:
Equation (4.42),
 ~ M + 2 × e × sin M + 1.25 × e2 × sin 2M
~ M + 2 × e × sin M + 1.25 × e2 × sin 2M
 ~ 2.53755 + 2 × 0.1 × sin(2.53755) + 1.25 × 0.12 × sin(2 × 2.53755)
~ 2.53755 + 2 × 0.1 × sin(2.53755) + 1.25 × 0.12 × sin(2 × 2.53755)
 ~ 2.63946 = 151.2 degrees
METHOD #2, High Accuracy:
Equation (4.41),
M = E - e × sin E
2.53755 = E - 0.1 × sin E
By iteration, E = 2.58996 radians
Equation (4.40),
cos E = (e + cos
~ 2.63946 = 151.2 degrees
METHOD #2, High Accuracy:
Equation (4.41),
M = E - e × sin E
2.53755 = E - 0.1 × sin E
By iteration, E = 2.58996 radians
Equation (4.40),
cos E = (e + cos  ) / (1 + e cos
) / (1 + e cos  )
Rearranging variables gives,
cos
)
Rearranging variables gives,
cos  = (cos E - e) / (1 - e cos E)
= (cos E - e) / (1 - e cos E)
 = arccos[(cos(2.58996) - 0.1) / (1 - 0.1 × cos(2.58996)]
= arccos[(cos(2.58996) - 0.1) / (1 - 0.1 × cos(2.58996)]
 = 2.64034 = 151.3 degrees
= 2.64034 = 151.3 degrees
PROBLEM 4.15
For the satellite in problems 4.13 and 4.14, calculate the length of its position
vector, its flight-path angle, and its velocity when the satellite's true anomaly
is 225 degrees.
SOLUTION,
Given: a = 7,500,000 m
e = 0.1
 = 225 degrees
Equations (4.43) and (4.44),
r = a × (1 - e2) / (1 + e × cos
= 225 degrees
Equations (4.43) and (4.44),
r = a × (1 - e2) / (1 + e × cos  )
r = 7,500,000 × (1 - 0.12) / (1 + 0.1 × cos(225))
r = 7,989,977 m
)
r = 7,500,000 × (1 - 0.12) / (1 + 0.1 × cos(225))
r = 7,989,977 m
 = arctan[ e × sin
= arctan[ e × sin  / (1 + e × cos
/ (1 + e × cos  )]
)]
 = arctan[ 0.1 × sin(225) / (1 + 0.1 × cos(225))]
= arctan[ 0.1 × sin(225) / (1 + 0.1 × cos(225))]
 = -4.351 degrees
Equation (4.45),
v = SQRT[ GM × (2 / r - 1 / a)]
v = SQRT[ 3.986005×1014 × (2 / 7,989,977 - 1 / 7,500,000)]
v = 6,828 m/s
= -4.351 degrees
Equation (4.45),
v = SQRT[ GM × (2 / r - 1 / a)]
v = SQRT[ 3.986005×1014 × (2 / 7,989,977 - 1 / 7,500,000)]
v = 6,828 m/s
PROBLEM 4.16
Calculate the perturbations in longitude of the ascending node and argument of
perigee caused by the Moon and Sun for the International Space Station orbiting
at an altitude of 400 km, an inclination of 51.6 degrees, and with an orbital
period of 92.6 minutes.
SOLUTION,
Given: i = 51.6 degrees
n = 1436 / 92.6 = 15.5 revolutions/day
Equations (4.46) through (4.49),
 Moon = -0.00338 × cos(i) / n
Moon = -0.00338 × cos(i) / n
 Moon = -0.00338 × cos(51.6) / 15.5
Moon = -0.00338 × cos(51.6) / 15.5
 Moon = -0.000135 deg/day
Moon = -0.000135 deg/day
 Sun = -0.00154 × cos(i) / n
Sun = -0.00154 × cos(i) / n
 Sun = -0.00154 × cos(51.6) / 15.5
Sun = -0.00154 × cos(51.6) / 15.5
 Sun = -0.0000617 deg/day
Sun = -0.0000617 deg/day
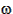 Moon = 0.00169 × (4 - 5 × sin2 i) / n
Moon = 0.00169 × (4 - 5 × sin2 i) / n
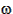 Moon = 0.00169 × (4 - 5 × sin2 51.6) / 15.5
Moon = 0.00169 × (4 - 5 × sin2 51.6) / 15.5
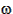 Moon = 0.000101 deg/day
Moon = 0.000101 deg/day
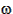 Sun = 0.00077 × (4 - 5 × sin2 i) / n
Sun = 0.00077 × (4 - 5 × sin2 i) / n
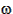 Sun = 0.00077 × (4 - 5 × sin2 51.6) / 15.5
Sun = 0.00077 × (4 - 5 × sin2 51.6) / 15.5
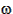 Sun = 0.000046 deg/day
Sun = 0.000046 deg/day
PROBLEM 4.17
A satellite is in an orbit with a semi-major axis of 7,500 km, an inclination
of 28.5 degrees, and an eccentricity of 0.1. Calculate the J2 perturbations in
longitude of the ascending node and argument of perigee.
SOLUTION,
Given: a = 7,500 km
i = 28.5 degrees
e = 0.1
Equations (4.50) and (4.51),
 J2 = -2.06474×1014 × a-7/2 × (cos i) × (1 - e2)-2
J2 = -2.06474×1014 × a-7/2 × (cos i) × (1 - e2)-2
 J2 = -2.06474×1014 × (7,500)-7/2 × (cos 28.5) × (1 - (0.1)2)-2
J2 = -2.06474×1014 × (7,500)-7/2 × (cos 28.5) × (1 - (0.1)2)-2
 J2 = -5.067 deg/day
J2 = -5.067 deg/day
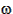 J2 = 1.03237×1014 × a-7/2 × (4 - 5 × sin2 i) × (1 - e2)-2
J2 = 1.03237×1014 × a-7/2 × (4 - 5 × sin2 i) × (1 - e2)-2
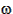 J2 = 1.03237×1014 × (7,500)-7/2 × (4 - 5 × sin2 28.5) × (1 - (0.1)2)-2
J2 = 1.03237×1014 × (7,500)-7/2 × (4 - 5 × sin2 28.5) × (1 - (0.1)2)-2
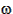 J2 = 8.250 deg/day
J2 = 8.250 deg/day
PROBLEM 4.18
A satellite is in a circular Earth orbit at an altitude of 400 km. The satellite
has a cylindrical shape 2 m in diameter by 4 m long and has a mass of 1,000 kg.
The satellite is traveling with its long axis perpendicular to the velocity
vector and it's drag coefficient is 2.67. Calculate the perturbations due to
atmospheric drag and estimate the satellite's lifetime.
SOLUTION,
Given: a = (6,378.14 + 400) × 1,000 = 6,778,140 m
A = 2 × 4 = 8 m2
m = 1,000 kg
CD = 2.67
From Atmosphere Properties,
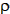 = 2.62×10-12 kg/m3
H = 58.2 km
Equation (4.6),
V = SQRT[ GM / a ]
V = SQRT[ 3.986005×1014 / 6,778,140 ]
V = 7,669 m/s
Equations (4.53) through (4.55),
= 2.62×10-12 kg/m3
H = 58.2 km
Equation (4.6),
V = SQRT[ GM / a ]
V = SQRT[ 3.986005×1014 / 6,778,140 ]
V = 7,669 m/s
Equations (4.53) through (4.55),
 arev = (-2 ×
arev = (-2 × 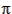 × CD × A ×
× CD × A × 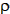 × a2) / m
× a2) / m
 arev = (-2 ×
arev = (-2 × 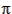 × 2.67 × 8 × 2.62×10-12 × 6,778,1402) / 1,000
× 2.67 × 8 × 2.62×10-12 × 6,778,1402) / 1,000
 arev = -16.2 m
arev = -16.2 m
 Prev = (-6 ×
Prev = (-6 × 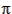 2 × CD × A ×
2 × CD × A × 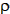 × a2) / (m × V)
× a2) / (m × V)
 Prev = (-6 ×
Prev = (-6 × 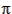 2 × 2.67 × 8 × 2.62×10-12 × 6,778,1402) / (1,000 × 7,669)
2 × 2.67 × 8 × 2.62×10-12 × 6,778,1402) / (1,000 × 7,669)
 Prev = -0.0199 s
Prev = -0.0199 s
 Vrev = (
Vrev = (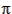 × CD × A ×
× CD × A × 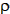 × a × V) / m
× a × V) / m
 Vrev = (
Vrev = (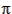 × 2.67 × 8 × 2.62×10-12 × 6,778,140 × 7,669) / 1,000
× 2.67 × 8 × 2.62×10-12 × 6,778,140 × 7,669) / 1,000
 Vrev = 0.00914 m/s
Equation (4.56),
L ~ -H /
Vrev = 0.00914 m/s
Equation (4.56),
L ~ -H /  arev
L ~ -(58.2 × 1,000) / -16.2
L ~ 3,600 revolutions
arev
L ~ -(58.2 × 1,000) / -16.2
L ~ 3,600 revolutions
PROBLEM 4.19
A spacecraft is in a circular parking orbit with an altitude of 200 km.
Calculate the velocity change required to perform a Hohmann transfer to a
circular orbit at geosynchronous altitude.
SOLUTION,
Given: rA = (6,378.14 + 200) × 1,000 = 6,578,140 m
From problem 4.3,
rB = 42,164,170 m
Equations (4.58) through (4.65),
atx = (rA + rB) / 2
atx = (6,578,140 + 42,164,170) / 2
atx = 24,371,155 m
ViA = SQRT[ GM / rA ]
ViA = SQRT[ 3.986005×1014 / 6,578,140 ]
ViA = 7,784 m/s
VfB = SQRT[ GM / rB ]
VfB = SQRT[ 3.986005×1014 / 42,164,170 ]
VfB = 3,075 m/s
VtxA = SQRT[ GM × (2 / rA - 1 / atx)]
VtxA = SQRT[ 3.986005×1014 × (2 / 6,578,140 - 1 / 24,371,155)]
VtxA = 10,239 m/s
VtxB = SQRT[ GM × (2 / rB - 1 / atx)]
VtxB = SQRT[ 3.986005×1014 × (2 / 42,164,170 - 1 / 24,371,155)]
VtxB = 1,597 m/s
 VA = VtxA - ViA
VA = VtxA - ViA
 VA = 10,239 - 7,784
VA = 10,239 - 7,784
 VA = 2,455 m/s
VA = 2,455 m/s
 VB = VfB - VtxB
VB = VfB - VtxB
 VB = 3,075 - 1,597
VB = 3,075 - 1,597
 VB = 1,478 m/s
VB = 1,478 m/s
 VT =
VT =  VA +
VA +  VB
VB
 VT = 2,455 + 1,478
VT = 2,455 + 1,478
 VT = 3,933 m/s
VT = 3,933 m/s
PROBLEM 4.20
A satellite is in a circular parking orbit with an altitude of 200 km. Using
a one-tangent burn, it is to be transferred to geosynchronous altitude using a
transfer ellipse with a semi-major axis of 30,000 km. Calculate the total
required velocity change and the time required to complete the transfer.
SOLUTION,
Given: rA = (6,378.14 + 200) × 1,000 = 6,578,140 m
rB = 42,164,170 m
atx = 30,000 × 1,000 = 30,000,000 m
Equations (4.66) through (4.68),
e = 1 - rA / atx
e = 1 - 6,578,140 / 30,000,000
e = 0.780729
 = arccos[(atx × (1 - e2) / rB - 1) / e ]
= arccos[(atx × (1 - e2) / rB - 1) / e ]
 = arccos[(30,000,000 × (1 - 0.7807292) / 42,164,170 - 1) / 0.780729 ]
= arccos[(30,000,000 × (1 - 0.7807292) / 42,164,170 - 1) / 0.780729 ]
 = 157.670 degrees
= 157.670 degrees
 = arctan[ e × sin
= arctan[ e × sin  / (1 + e × cos
/ (1 + e × cos  )]
)]
 = arctan[ 0.780729 × sin(157.670) / (1 + 0.780729 × cos(157.670))]
= arctan[ 0.780729 × sin(157.670) / (1 + 0.780729 × cos(157.670))]
 = 46.876 degrees
Equations (4.59) through (4.63),
ViA = SQRT[ GM / rA ]
ViA = SQRT[ 3.986005×1014 / 6,578,140 ]
ViA = 7,784 m/s
VfB = SQRT[ GM / rB ]
VfB = SQRT[ 3.986005×1014 / 42,164,170 ]
VfB = 3,075 m/s
VtxA = SQRT[ GM × (2 / rA - 1 / atx)]
VtxA = SQRT[ 3.986005×1014 × (2 / 6,578,140 - 1 / 30,000,000)]
VtxA = 10,388 m/s
VtxB = SQRT[ GM × (2 / rB - 1 / atx)]
VtxB = SQRT[ 3.986005×1014 × (2 / 42,164,170 - 1 / 30,000,000)]
VtxB = 2,371 m/s
= 46.876 degrees
Equations (4.59) through (4.63),
ViA = SQRT[ GM / rA ]
ViA = SQRT[ 3.986005×1014 / 6,578,140 ]
ViA = 7,784 m/s
VfB = SQRT[ GM / rB ]
VfB = SQRT[ 3.986005×1014 / 42,164,170 ]
VfB = 3,075 m/s
VtxA = SQRT[ GM × (2 / rA - 1 / atx)]
VtxA = SQRT[ 3.986005×1014 × (2 / 6,578,140 - 1 / 30,000,000)]
VtxA = 10,388 m/s
VtxB = SQRT[ GM × (2 / rB - 1 / atx)]
VtxB = SQRT[ 3.986005×1014 × (2 / 42,164,170 - 1 / 30,000,000)]
VtxB = 2,371 m/s
 VA = VtxA - ViA
VA = VtxA - ViA
 VA = 10,388 - 7,784
VA = 10,388 - 7,784
 VA = 2,604 m/s
Equation (4.69),
VA = 2,604 m/s
Equation (4.69),
 VB = SQRT[ VtxB2 + VfB2 - 2 × VtxB × VfB × cos
VB = SQRT[ VtxB2 + VfB2 - 2 × VtxB × VfB × cos  ]
]
 VB = SQRT[ 2,3712 + 3,0752 - 2 × 2,371 × 3,075 × cos(46.876)]
VB = SQRT[ 2,3712 + 3,0752 - 2 × 2,371 × 3,075 × cos(46.876)]
 VB = 2,260 m/s
Equation (4.65),
VB = 2,260 m/s
Equation (4.65),
 VT =
VT =  VA +
VA +  VB
VB
 VT = 2,604 + 2,260
VT = 2,604 + 2,260
 VT = 4,864 m/s
Equations (4.70) and (4.71),
E = arccos[(e + cos
VT = 4,864 m/s
Equations (4.70) and (4.71),
E = arccos[(e + cos  ) / (1 + e cos
) / (1 + e cos  )]
E = arccos[(0.780729 + cos(157.670)) / (1 + 0.780729 × cos(157.670))]
E = 2.11688 radians
TOF = (E - e × sin E) × SQRT[ atx3 / GM ]
TOF = (2.11688 - 0.780729 × sin(2.11688)) × SQRT[ 30,000,0003 / 3.986005×1014 ]
TOF = 11,931 s = 3.314 hours
)]
E = arccos[(0.780729 + cos(157.670)) / (1 + 0.780729 × cos(157.670))]
E = 2.11688 radians
TOF = (E - e × sin E) × SQRT[ atx3 / GM ]
TOF = (2.11688 - 0.780729 × sin(2.11688)) × SQRT[ 30,000,0003 / 3.986005×1014 ]
TOF = 11,931 s = 3.314 hours
PROBLEM 4.21
Calculate the velocity change required to transfer a satellite from a circular
600 km orbit with an inclination of 28 degrees to an orbit of equal size with
an inclination of 20 degrees.
SOLUTION,
Given: r = (6,378.14 + 600) × 1,000 = 6,978,140 m
 = 28 - 20 = 8 degrees
Equation (4.6),
Vi = SQRT[ GM / r ]
Vi = SQRT[ 3.986005×1014 / 6,978,140 ]
Vi = 7,558 m/s
Equation (4.73),
= 28 - 20 = 8 degrees
Equation (4.6),
Vi = SQRT[ GM / r ]
Vi = SQRT[ 3.986005×1014 / 6,978,140 ]
Vi = 7,558 m/s
Equation (4.73),
 V = 2 × Vi × sin(
V = 2 × Vi × sin( /2)
/2)
 V = 2 × 7,558 × sin(8/2)
V = 2 × 7,558 × sin(8/2)
 V = 1,054 m/s
V = 1,054 m/s
PROBLEM 4.22
A satellite is in a parking orbit with an altitude of 200 km and an inclination
of 28 degrees. Calculate the total velocity change required to transfer the
satellite to a zero-inclination geosynchronous orbit using a Hohmann transfer
with a combined plane change at apogee.
Given: rA = (6,378.14 + 200) × 1,000 = 6,578,140 m
rB = 42,164,170 m
 = 28 degrees
From problem 4.19,
VfB = 3,075 m/s
VtxB = 1,597 m/s
= 28 degrees
From problem 4.19,
VfB = 3,075 m/s
VtxB = 1,597 m/s
 VA = 2,455 m/s
Equation (4.74),
VA = 2,455 m/s
Equation (4.74),
 VB = SQRT[ VtxB2 + VfB2 - 2 × VtxB × VfB × cos
VB = SQRT[ VtxB2 + VfB2 - 2 × VtxB × VfB × cos  ]
]
 VB = SQRT[ 1,5972 + 3,0752 - 2 × 1,597 × 3,075 × cos(28)]
VB = SQRT[ 1,5972 + 3,0752 - 2 × 1,597 × 3,075 × cos(28)]
 VB = 1,826 m/s
Equation (4.65),
VB = 1,826 m/s
Equation (4.65),
 VT =
VT =  VA +
VA +  VB
VB
 VT = 2,455 + 1,826
VT = 2,455 + 1,826
 VT = 4,281 m/s
VT = 4,281 m/s
PROBLEM 4.23
A spacecraft is in an orbit with an inclination of 30 degrees and the longitude
of the ascending node is 75 degrees. Calculate the angle change required to
change the inclination to 32 degrees and the longitude of the ascending node to
80 degrees.
SOLUTION,
Given: ii = 30 degrees
 i = 75 degrees
if = 32 degrees
i = 75 degrees
if = 32 degrees
 f = 80 degrees
Equation (4.75),
a1 = sin(ii)cos(
f = 80 degrees
Equation (4.75),
a1 = sin(ii)cos( i) = sin(30)cos(75) = 0.129410
a2 = sin(ii)sin(
i) = sin(30)cos(75) = 0.129410
a2 = sin(ii)sin( i) = sin(30)sin(75) = 0.482963
a3 = cos(ii) = cos(30) = 0.866025
b1 = sin(if)cos(
i) = sin(30)sin(75) = 0.482963
a3 = cos(ii) = cos(30) = 0.866025
b1 = sin(if)cos( f) = sin(32)cos(80) = 0.0920195
b2 = sin(if)sin(
f) = sin(32)cos(80) = 0.0920195
b2 = sin(if)sin( f) = sin(32)sin(80) = 0.521869
b3 = cos(if) = cos(32) = 0.848048
f) = sin(32)sin(80) = 0.521869
b3 = cos(if) = cos(32) = 0.848048
 = arccos(a1 × b1 + a2 × b2 + a3 × b3)
= arccos(a1 × b1 + a2 × b2 + a3 × b3)
 = arccos(0.129410 × 0.0920195 + 0.482963 × 0.521869 + 0.866025 × 0.848048)
= arccos(0.129410 × 0.0920195 + 0.482963 × 0.521869 + 0.866025 × 0.848048)
 = 3.259 degrees
= 3.259 degrees
PROBLEM 4.24
Calculate the latitude and longitude of the intersection nodes between the
initial and final orbits for the spacecraft in problem 4.23.
SOLUTION,
From problem 4.21,
a1 = 0.129410
a2 = 0.482963
a3 = 0.866025
b1 = 0.0920195
b2 = 0.521869
b3 = 0.848048
Equations (4.76) and (4.77),
c1 = a2 × b3 - a3 × b2 = 0.482963 × 0.848048 - 0.866025 × 0.521869 = -0.0423757
c2 = a3 × b1 - a1 × b3 = 0.866025 × 0.0920195 - 0.129410 × 0.848048 = -0.0300543
c3 = a1 × b2 - a2 × b1 = 0.129410 × 0.521869 - 0.482963 × 0.0920195 = 0.0230928
lat1 = arctan(c3 / (c12 + c22)1/2)
lat1 = arctan(0.0230928 / (-0.04237572 + -0.03005432)1/2)
lat1 = 23.965 degrees
long1 = arctan(c2 / c1) + 90
long1 = arctan(-0.0300543 / -0.0423757) + 90
long1 = 125.346 degrees
lat2 = -23.965 degrees
long2 = 125.346 + 180 = 305.346 degrees
PROBLEM 4.25
Calculate the escape velocity of a spacecraft launched from an Earth orbit with
an altitude of 200 km.
SOLUTION,
Given: r = (6,378.14 + 200) × 1,000 = 6,578,140 m
Equation (4.78),
Vesc = SQRT[ 2 × GM / r ]
Vesc = SQRT[ 2 × 3.986005×1014 / 6,578,140 ]
Vesc = 11,009 m/s
PROBLEM 4.26
A space probe is approaching Mars on a hyperbolic flyby trajectory. When at
a distance of 100,000 km, its velocity relative to Mars is 5,140.0 m/s and
its flight path angle is -85.300 degrees. Calculate the probe's eccentricity,
semi-major axis, turning angle, angle 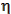 , true anomaly, impact parameter,
periapsis radius, and parameter p.
SOLUTION,
From Basics Constants,
GM of Mars = 4.282831×1013 m3/s2
Given: r = 100,000 × 1,000 = 100,000,000 m
v = 5,140.0 m/s
, true anomaly, impact parameter,
periapsis radius, and parameter p.
SOLUTION,
From Basics Constants,
GM of Mars = 4.282831×1013 m3/s2
Given: r = 100,000 × 1,000 = 100,000,000 m
v = 5,140.0 m/s
 = -85.300o
Equations (4.30) and (4.32),
e = SQRT[ (r × v2 / GM - 1)2 × cos2
= -85.300o
Equations (4.30) and (4.32),
e = SQRT[ (r × v2 / GM - 1)2 × cos2  + sin2
+ sin2  ]
e = SQRT[ (100,000,000 × 5,1402 / 4.282831×1013 - 1)2 × cos2(-85.3) + sin2(-85.3) ]
e = 5.0715
a = 1 / ( 2 / r - v2 / GM )
a = 1 / ( 2 / 100,000,000 - 5,1402 / 4.282831×1013 )
a = -1,675,400 m
Equations (4.80) through (4.85),
sin(
]
e = SQRT[ (100,000,000 × 5,1402 / 4.282831×1013 - 1)2 × cos2(-85.3) + sin2(-85.3) ]
e = 5.0715
a = 1 / ( 2 / r - v2 / GM )
a = 1 / ( 2 / 100,000,000 - 5,1402 / 4.282831×1013 )
a = -1,675,400 m
Equations (4.80) through (4.85),
sin(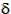 /2) = 1 / e
/2) = 1 / e
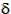 = 2 × arcsin( 1 / 5.0715 )
= 2 × arcsin( 1 / 5.0715 )
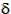 = 22.744o
cos
= 22.744o
cos 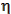 = -1 / e
= -1 / e
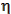 = arccos( -1 / 5.0715 )
= arccos( -1 / 5.0715 )
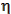 = 101.37o
= 101.37o
 = arccos[ (a × (1 - e2) - r) / (e × r) ]
= arccos[ (a × (1 - e2) - r) / (e × r) ]
 = arccos[ (-1,675,400 × (1 - 5.07152) - 100,000,000) / (5.0715 × 100,000,000) ]
= arccos[ (-1,675,400 × (1 - 5.07152) - 100,000,000) / (5.0715 × 100,000,000) ]
 = -96.633o
b = -a / tan(
= -96.633o
b = -a / tan(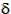 /2)
b = 1,675.4 / tan(22.744/2)
b = 8,330.0 km
ro = a × (1 - e)
ro = -1,675.4 × (1 - 5.0715)
ro = 6,821.4 km
p = a × (1 - e2)
p = -1,675.4 × (1 - 5.07152)
p = 41,416 km
/2)
b = 1,675.4 / tan(22.744/2)
b = 8,330.0 km
ro = a × (1 - e)
ro = -1,675.4 × (1 - 5.0715)
ro = 6,821.4 km
p = a × (1 - e2)
p = -1,675.4 × (1 - 5.07152)
p = 41,416 km
PROBLEM 4.27
The space probe in problem 4.26 has moved to a true anomaly of 75 degrees.
Calculate the radius vector, flight path angle, and velocity.
SOLUTION,
Given: a = -1,675,400 m
e = 5.0715
 = 75o
Equations (4.43) through (4.45),
r = a × (1 - e2) / (1 + e × cos
= 75o
Equations (4.43) through (4.45),
r = a × (1 - e2) / (1 + e × cos  )
r = -1,675,400 × (1 - 5.07152) / (1 + 5.0715 × cos(75))
r = 17,909,000 m
)
r = -1,675,400 × (1 - 5.07152) / (1 + 5.0715 × cos(75))
r = 17,909,000 m
 = arctan[ e × sin
= arctan[ e × sin  / (1 + e × cos
/ (1 + e × cos  )]
)]
 = arctan[ 5.0715 × sin(75) / (1 + 5.0715 × cos(75))]
= arctan[ 5.0715 × sin(75) / (1 + 5.0715 × cos(75))]
 = 64.729o
v = SQRT[ GM × (2 / r - 1 / a)]
v = SQRT[ 4.282831×1013 × (2 / 17,909,000 - 1 / -1,675,400)]
v = 5,508.7 m/s
= 64.729o
v = SQRT[ GM × (2 / r - 1 / a)]
v = SQRT[ 4.282831×1013 × (2 / 17,909,000 - 1 / -1,675,400)]
v = 5,508.7 m/s
PROBLEM 4.28
A spacecraft is launched from Earth on a hyperbolic trajectory with a semi-major
axis of -36,000 km and an eccentricity of 1.1823. How long does it take to move
from a true anomaly of 15 degrees to a true anomaly of 120 degrees?
SOLUTION,
Given: a = -36,000 × 1,000 = -36,000,000 m
e = 1.1823
 O = 15o
O = 15o
 = 120o
Equation (4.87),
cosh F = (e + cos
= 120o
Equation (4.87),
cosh F = (e + cos  ) / (1 + e cos
) / (1 + e cos  )
Fo = arccosh[(1.1823 + cos(15)) / (1 + 1.1823 × cos(15))]
Fo = 0.07614
F = arccosh[(1.1823 + cos(120)) / (1 + 1.1823 × cos(120))]
F = 1.10023
Equation (4.86),
t - tO = SQRT[(-a)3 / GM ] × [(e × sinh F - F) - (e × sinh Fo - Fo)]
t - tO = SQRT[(36,000,000)3 / 3.986005×1014 ] × [(1.1823 × sinh(1.10023) - 1.10023)
- (1.1823 × sinh(0.07614) - 0.07614)]
t - tO = 5,035 s = 1.399 hours
)
Fo = arccosh[(1.1823 + cos(15)) / (1 + 1.1823 × cos(15))]
Fo = 0.07614
F = arccosh[(1.1823 + cos(120)) / (1 + 1.1823 × cos(120))]
F = 1.10023
Equation (4.86),
t - tO = SQRT[(-a)3 / GM ] × [(e × sinh F - F) - (e × sinh Fo - Fo)]
t - tO = SQRT[(36,000,000)3 / 3.986005×1014 ] × [(1.1823 × sinh(1.10023) - 1.10023)
- (1.1823 × sinh(0.07614) - 0.07614)]
t - tO = 5,035 s = 1.399 hours
PROBLEM 4.29
A spacecraft launched from Earth has a burnout velocity of 11,500 m/s at an
altitude of 200 km. What is the hyperbolic excess velocity?
SOLUTION,
Given: Vbo = 11,500 m/s
From problem 4.25,
Vesc = 11,009 m/s
Equation (4.88),
V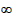 2 = Vbo2 - Vesc2
V
2 = Vbo2 - Vesc2
V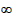 = SQRT[ 11,5002 - 11,0092 ]
V
= SQRT[ 11,5002 - 11,0092 ]
V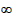 = 3,325 m/s
= 3,325 m/s
PROBLEM 4.30
Calculate the radius of Earth's sphere of influence.
SOLUTION,
From Basics Constants,
Dsp = 149,597,870 km
MP = 5.9737×1024 kg
MS = 1.9891×1030 kg
Equation (4.89),
REarth = Dsp × (MP / MS)0.4
REarth = 149,597,870 × (5.9737×1024 / 1.9891×1030)0.4
REarth = 925,000 km
PROBLEM 5.1
Using a one-tangent burn, calculate the change in true anomaly and the
time-of-flight for a transfer from Earth to Mars. The radius vector of Earth at
departure is 1.000 AU and that of Mars at arrival is 1.524 AU. The semi-major
axis of the transfer orbit is 1.300 AU.
SOLUTION,
Given: rA = 1.000 AU
rB = 1.524 AU
atx = 1.300 AU × 149.597870×109 m/AU = 194.48×109 m
From Basics Constants,
GM of Sun = 1.327124×1020 m3/s2
Equations (4.66) and (4.67),
e = 1 - rA / atx
e = 1 - 1.0 / 1.3
e = 0.230769
 = arccos[(atx × (1 - e2) / rB - 1) / e ]
= arccos[(atx × (1 - e2) / rB - 1) / e ]
 = arccos[(1.3 × (1 - 0.2307692) / 1.524 - 1) / 0.230769 ]
= arccos[(1.3 × (1 - 0.2307692) / 1.524 - 1) / 0.230769 ]
 = 146.488 degrees
Equations (4.70) and (4.71),
E = arccos[(e + cos
= 146.488 degrees
Equations (4.70) and (4.71),
E = arccos[(e + cos  ) / (1 + e cos
) / (1 + e cos  )]
E = arccos[(0.230769 + cos(146.488)) / (1 + 0.230769 × cos(146.488))]
E = 2.41383 radians
TOF = (E - e × sin E) × SQRT[ atx3 / GM ]
TOF = (2.41383 - 0.230769 × sin(2.41383)) × SQRT[ (194.48×109)3 / 1.327124×1020 ]
TOF = 16,827,800 s = 194.77 days
)]
E = arccos[(0.230769 + cos(146.488)) / (1 + 0.230769 × cos(146.488))]
E = 2.41383 radians
TOF = (E - e × sin E) × SQRT[ atx3 / GM ]
TOF = (2.41383 - 0.230769 × sin(2.41383)) × SQRT[ (194.48×109)3 / 1.327124×1020 ]
TOF = 16,827,800 s = 194.77 days
PROBLEM 5.2
For the transfer orbit in problem 5.1, calculate the departure phase angle, given
that the angular velocity of Mars is 0.5240 degrees/day.
SOLUTION,
Given:  2-
2- 1 = 146.488o
t2-t1 = 194.77 days
1 = 146.488o
t2-t1 = 194.77 days
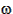 t = 0.5240o/day
Equation (5.1),
t = 0.5240o/day
Equation (5.1),
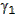 = (
= ( 2-
2- 1) -
1) - 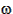 t × (t2-t1)
t × (t2-t1)
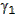 = 146.488 - 0.5240 × 194.77
= 146.488 - 0.5240 × 194.77
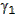 = 44.43o
= 44.43o
PROBLEM 5.3
A flight to Mars is launched on 2020-7-20, 0:00 UT. The planned time of flight
is 207 days. Earth's postion vector at departure is 0.473265X - 0.899215Y AU.
Mars' postion vector at intercept is 0.066842X + 1.561256Y + 0.030948Z AU.
Calculate the parameter and semi-major axis of the transfer orbit.
SOLUTION,
Given: t = 207 days
r1 = 0.473265X - 0.899215Y AU
r2 = 0.066842X + 1.561256Y + 0.030948Z AU
GM = 1.327124×1020 m3/s2
= 1.327124×1020 / (149.597870×109)3 = 3.964016×10-14 AU3/s2
From vector magnitude,
r1 = SQRT[ 0.4732652 + (-0.899215)2 ]
r1 = 1.016153 AU
r2 = SQRT[ 0.0668422 + 1.5612562 + 0.0309482 ]
r2 = 1.562993 AU
From vector dot product,

 = arccos[ (0.473265 × 0.066842 - 0.899215 × 1.561256) / (1.016153 × 1.562993) ]
= arccos[ (0.473265 × 0.066842 - 0.899215 × 1.561256) / (1.016153 × 1.562993) ]

 = 149.770967o
Equations (5.9), (5.10) and (5.11),
k = r1 × r2 × (1 - cos
= 149.770967o
Equations (5.9), (5.10) and (5.11),
k = r1 × r2 × (1 - cos 
 )
k = 1.016153 × 1.562993 × (1 - cos(149.770967))
k = 2.960511 AU
)
k = 1.016153 × 1.562993 × (1 - cos(149.770967))
k = 2.960511 AU
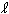 = r1 + r2
= r1 + r2
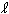 = 1.016153 + 1.562993
= 1.016153 + 1.562993
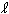 = 2.579146 AU
m = r1 × r2 × (1 + cos
= 2.579146 AU
m = r1 × r2 × (1 + cos 
 )
m = 1.016153 × 1.562993 × (1 + cos(149.770967))
m = 0.215969 AU
Equations (5.18) and (5.19),
pi = k / (
)
m = 1.016153 × 1.562993 × (1 + cos(149.770967))
m = 0.215969 AU
Equations (5.18) and (5.19),
pi = k / (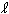 + SQRT(2 × m))
pi = 2.960511 / (2.579146 + SQRT(2 × 0.215969))
pi = 0.914764 AU
pii = k / (
+ SQRT(2 × m))
pi = 2.960511 / (2.579146 + SQRT(2 × 0.215969))
pi = 0.914764 AU
pii = k / (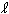 - SQRT(2 × m))
pii = 2.960511 / (2.579146 - SQRT(2 × 0.215969))
pii = 1.540388 AU
Since
- SQRT(2 × m))
pii = 2.960511 / (2.579146 - SQRT(2 × 0.215969))
pii = 1.540388 AU
Since 
 <
< 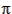 , 0.914764 < p <
, 0.914764 < p < 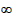 Equation (5.12),
Select trial value, p = 1.2 AU
a = m × k × p / [(2 × m -
Equation (5.12),
Select trial value, p = 1.2 AU
a = m × k × p / [(2 × m - 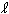 2) × p2 + 2 × k ×
2) × p2 + 2 × k × 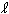 × p - k2]
a = 0.215969 × 2.960511 × 1.2
/ [(2 × 0.215969 - 2.5791462) × 1.22 + 2 × 2.960511 × 2.579146 × 1.2 - 2.9605112]
a = 1.270478 AU
Equations (5.5), (5.6) and (5.7),
f = 1 - r2 / p × (1 - cos
× p - k2]
a = 0.215969 × 2.960511 × 1.2
/ [(2 × 0.215969 - 2.5791462) × 1.22 + 2 × 2.960511 × 2.579146 × 1.2 - 2.9605112]
a = 1.270478 AU
Equations (5.5), (5.6) and (5.7),
f = 1 - r2 / p × (1 - cos 
 )
f = 1 - 1.562993 / 1.2 × (1 - cos(149.770967))
f = -1.427875
g = r1 × r2 × sin
)
f = 1 - 1.562993 / 1.2 × (1 - cos(149.770967))
f = -1.427875
g = r1 × r2 × sin 
 / SQRT[ GM × p ]
g = 1.016153 × 1.562993 × sin(149.770967) / SQRT[ 3.964016×10-14 × 1.2 ]
g = 3,666,240
/ SQRT[ GM × p ]
g = 1.016153 × 1.562993 × sin(149.770967) / SQRT[ 3.964016×10-14 × 1.2 ]
g = 3,666,240
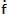 = SQRT[ GM / p ] × tan(
= SQRT[ GM / p ] × tan(
 /2) × [(1 - cos
/2) × [(1 - cos 
 ) / p - 1/r1 - 1/r2 ]
) / p - 1/r1 - 1/r2 ]
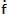 = SQRT[ 3.964016×10-14 / 1.2 ] × tan(149.770967/2)
× [(1 - cos(149.770967)) / 1.2 - 1/1.016153 - 1/1.562993 ]
= SQRT[ 3.964016×10-14 / 1.2 ] × tan(149.770967/2)
× [(1 - cos(149.770967)) / 1.2 - 1/1.016153 - 1/1.562993 ]
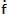 = -4.747601×10-8
Equation (5.13),
= -4.747601×10-8
Equation (5.13),
 E = arccos[ 1 - r1 / a × (1 - f) ]
E = arccos[ 1 - r1 / a × (1 - f) ]
 E = arccos[ 1 - 1.016153 / 1.270478 × (1 + 1.427875) ]
E = arccos[ 1 - 1.016153 / 1.270478 × (1 + 1.427875) ]
 E = 2.798925 radians
Equation (5.16),
t = g + SQRT[ a3 / GM ] × (
E = 2.798925 radians
Equation (5.16),
t = g + SQRT[ a3 / GM ] × ( E - sin
E - sin  E)
t = 3,666,240 + SQRT[ 1.2704783 / 3.964016×10-14 ] × (2.798925 - sin(2.798925))
t = 21,380,951 s = 247.4647 days
Select new trial value of p and repeat above steps,
p = 1.300000 AU, a = 1.443005 AU, t = 178.9588 days
Equation (5.20),
pn+1 = pn + (t - tn) × (pn - pn-1) / (tn - tn-1)
pn+1 = 1.3 + (207 - 178.9588) × (1.3 - 1.2) / (178.9588 - 247.4647)
pn+1 = 1.259067 AU
Recalculate using new value of p,
p = 1.259067 AU, a = 1.336197 AU, t = 201.5624 days
Perform additional iterations,
p = 1.249221 AU, a = 1.318624 AU, t = 207.9408 days
p = 1.250673 AU, a = 1.321039 AU, t = 206.9733 days
p = 1.250633 AU, a = 1.320971 AU, t = 206.9999 days <-- close enough
E)
t = 3,666,240 + SQRT[ 1.2704783 / 3.964016×10-14 ] × (2.798925 - sin(2.798925))
t = 21,380,951 s = 247.4647 days
Select new trial value of p and repeat above steps,
p = 1.300000 AU, a = 1.443005 AU, t = 178.9588 days
Equation (5.20),
pn+1 = pn + (t - tn) × (pn - pn-1) / (tn - tn-1)
pn+1 = 1.3 + (207 - 178.9588) × (1.3 - 1.2) / (178.9588 - 247.4647)
pn+1 = 1.259067 AU
Recalculate using new value of p,
p = 1.259067 AU, a = 1.336197 AU, t = 201.5624 days
Perform additional iterations,
p = 1.249221 AU, a = 1.318624 AU, t = 207.9408 days
p = 1.250673 AU, a = 1.321039 AU, t = 206.9733 days
p = 1.250633 AU, a = 1.320971 AU, t = 206.9999 days <-- close enough
PROBLEM 5.4
For the Mars transfer orbit in Problem 5.3, calculate the departure and intecept
velocity vectors.
SOLUTION,
Given: r1 = 0.473265X - 0.899215Y AU
r2 = 0.066842X + 1.561256Y + 0.030948Z AU
r1 = 1.016153 AU
r2 = 1.562993 AU
p = 1.250633 AU
a = 1.320971 AU

 = 149.770967o
Equations (5.5), (5.6) and (5.7),
f = 1 - r2 / p × (1 - cos
= 149.770967o
Equations (5.5), (5.6) and (5.7),
f = 1 - r2 / p × (1 - cos 
 )
f = 1 - 1.562993 / 1.250633 × (1 - cos(149.770967))
f = -1.329580
g = r1 × r2 × sin
)
f = 1 - 1.562993 / 1.250633 × (1 - cos(149.770967))
f = -1.329580
g = r1 × r2 × sin 
 / SQRT[ GM × p ]
g = 1.016153 × 1.562993 × sin(149.770967) / SQRT[ 3.964016×10-14 × 1.250633 ]
g = 3,591,258
/ SQRT[ GM × p ]
g = 1.016153 × 1.562993 × sin(149.770967) / SQRT[ 3.964016×10-14 × 1.250633 ]
g = 3,591,258
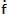 = SQRT[ GM / p ] × tan(
= SQRT[ GM / p ] × tan(
 /2) × [(1 - cos
/2) × [(1 - cos 
 ) / p - 1/r1 - 1/r2 ]
) / p - 1/r1 - 1/r2 ]
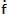 = SQRT[ 3.964016×10-14 / 1.250633 ] × tan(149.770967/2)
× [(1 - cos(149.770967)) / 1.250633 - 1/1.016153 - 1/1.562993 ]
= SQRT[ 3.964016×10-14 / 1.250633 ] × tan(149.770967/2)
× [(1 - cos(149.770967)) / 1.250633 - 1/1.016153 - 1/1.562993 ]
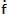 = -8.795872×10-8
= -8.795872×10-8
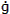 = 1 - r1 / p × (1 - cos
= 1 - r1 / p × (1 - cos 
 )
)
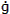 = 1 - 1.016153 / 1.250633 × (1 - cos(149.770967))
= 1 - 1.016153 / 1.250633 × (1 - cos(149.770967))
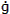 = -0.514536
Equation (5.3),
v1 = (r2 - f × r1) / g
v1 = [(0.066842 + 1.329580 × 0.473265) / 3,591,258] X
+ [(1.561256 + 1.329580 × -0.899215) / 3,591,258] Y
+ [(0.030948 + 1.329580 × 0) / 3,591,258] Z
v1 = 0.000000193828X + 0.000000101824Y + 0.00000000861759Z AU/s × 149.597870×109
v1 = 28996.2X + 15232.7Y + 1289.2Z m/s
Equation (5.4),
v2 =
= -0.514536
Equation (5.3),
v1 = (r2 - f × r1) / g
v1 = [(0.066842 + 1.329580 × 0.473265) / 3,591,258] X
+ [(1.561256 + 1.329580 × -0.899215) / 3,591,258] Y
+ [(0.030948 + 1.329580 × 0) / 3,591,258] Z
v1 = 0.000000193828X + 0.000000101824Y + 0.00000000861759Z AU/s × 149.597870×109
v1 = 28996.2X + 15232.7Y + 1289.2Z m/s
Equation (5.4),
v2 = 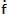 × r1 +
× r1 + 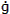 × v1
v2 = [-8.795872×10-8 × 0.473265 - 0.514536 × 0.000000193828] X
+ [-8.795872×10-8 × -0.899215 - 0.514536 × 0.000000101824] Y
+ [-8.795872×10-8 × 0 - 0.514536 × 0.00000000861759] Z
v2 = -0.000000141359X + 0.0000000267017Y - 0.00000000443406Z AU/s × 149.597870×109
v2 = -21147.0X + 3994.5Y - 663.3Z m/s
× v1
v2 = [-8.795872×10-8 × 0.473265 - 0.514536 × 0.000000193828] X
+ [-8.795872×10-8 × -0.899215 - 0.514536 × 0.000000101824] Y
+ [-8.795872×10-8 × 0 - 0.514536 × 0.00000000861759] Z
v2 = -0.000000141359X + 0.0000000267017Y - 0.00000000443406Z AU/s × 149.597870×109
v2 = -21147.0X + 3994.5Y - 663.3Z m/s
PROBLEM 5.5
For the Mars transfer orbit in Problems 5.3 and 5.4, calculate the orbital elements.
SOLUTION,
Problem can be solved using either r1 & v1 or r2 & v2 – we will use r1 & v1.
Given: r1 = (0.473265X - 0.899215Y AU) × 149.597870×109 m/AU
= 7.079944×1010X - 1.345206×1011Y m
r1 = 1.016153 × 149.597870×109 = 1.520144×1011 m
GM = 1.327124×1020 m3/s2
From problem 5.4,
v1 = 28996.2X + 15232.7Y + 1289.2Z m/s
Also,
v = SQRT[ 28996.22 + 15232.72 + 1289.22 ] = 32,779.2 m/s
Equations (5.21) and (5.22),
h = (rY vZ - rZ vY)X + (rZ vX - rX vZ)Y + (rX vY - rY vX)Z
h = (-1.345206×1011 × 1289.2 - 0 × 15232.7)X + (0 × 28996.2 - 7.079944×1010 × 1289.2)Y
+ (7.079944×1010 × 15232.7 + 1.345206×1011 × 28996.2)Z
h = -1.73424×1014X - 9.12746×1013Y + 4.97905×1015Z
n = -hY X + hX Y
n = 9.12746×1013X - 1.73424×1014Y
Also,
h = SQRT[ (-1.73424×1014)2 + (-9.12746×1013)2 + (4.97905×1015)2 ] = 4.98291×1015
n = SQRT[ (9.12746×1013)2 + (1.73424×1014)2 ] = 1.95977×1014
Equation (5.23),
e = [(v2 - GM / r) × r - (r • v) × v ] / GM
v2 - GM / r = 32779.22 - 1.327124×1020 / 1.520144×1011 = 2.01451×108
r • v = 7.079944×1010 × 28996.2 - 1.345206×1011 × 15232.7 + 0 x 1289.2 = 3.80278×1012
e = [2.01451×108 × (7.079944×1010X - 1.345206×1011Y)
- 3.80278×1012 × (28996.2X + 15232.7Y + 1289.2Z) ] / 1.327124×1020
e = 0.106639X - 0.204632Y - 0.000037Z
Equations (5.24) and (5.25),
a = 1 / ( 2 / r - v2 / GM )
a = 1 / ( 2 / 1.520144×1011 - 32779.22 / 1.327124×1020 )
a = 1.97614×1011 m
e = SQRT[ 0.1066392 + (-0.204632)2 + (-0.000037)2 ]
e = 0.230751
Equations (5.26) though (5.30),
cos i = hZ / h
cos i = 4.97905×1015 / 4.98291×1015
i = 2.255o
cos  = nX / n
cos
= nX / n
cos  = 9.12746×1013 / 1.95977×1014
= 9.12746×1013 / 1.95977×1014
 = 297.76o
cos
= 297.76o
cos 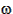 = n • e / (n × e)
cos
= n • e / (n × e)
cos 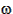 = (9.12746×1013 × 0.106639 - 1.73424×1014 × (-0.204632) + 0 × (-0.000037))
/ (1.95977×1014 × 0.230751)
= (9.12746×1013 × 0.106639 - 1.73424×1014 × (-0.204632) + 0 × (-0.000037))
/ (1.95977×1014 × 0.230751)
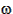 = 359.77o
cos
= 359.77o
cos  o = e • r / (e × r)
cos
o = e • r / (e × r)
cos  o = (0.106639 × 7.079944×1010 - 0.204632 × (-1.345206×1011) - 0.000037 × 0)
/ (0.230751 × 1.520144×1011)
o = (0.106639 × 7.079944×1010 - 0.204632 × (-1.345206×1011) - 0.000037 × 0)
/ (0.230751 × 1.520144×1011)
 o = 0.226o
cos uo = n • r / (n × r)
uo = 0 (launch point = ascending node)
Equations (5.31) and (5.32),
o = 0.226o
cos uo = n • r / (n × r)
uo = 0 (launch point = ascending node)
Equations (5.31) and (5.32),
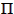 =
=  +
+ 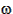
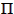 = 297.76 + 359.77
= 297.76 + 359.77
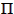 = 297.53o
= 297.53o
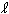 o =
o =  +
+ 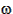 +
+  o
o
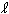 o = 297.76 + 359.77 + 0.23
o = 297.76 + 359.77 + 0.23
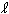 o = 297.76o
o = 297.76o
PROBLEM 5.6
For the spacecraft in Problems 5.3 and 5.4, calculate the hyperbolic excess
velocity at departure, the injection  V, and the zenith angle of the departure
asymptote. Injection occurs from an 200 km parking orbit. Earth's velocity
vector at departure is 25876.6X + 13759.5Y m/s.
SOLUTION,
Given: ro = (6,378.14 + 200) × 1,000 = 6,578,140 m
r = 0.473265X - 0.899215Y AU
VP = 25876.6X + 13759.5Y m/s
From problem 5.4,
VS = 28996.2X + 15232.7Y + 1289.2Z m/s
Equation (5.33),
VS/P = (VSX - VPX)X + (VSY - VPY)Y + (VSZ - VPZ)Z
VS/P = (28996.2 - 25876.6)X + (15232.7 - 13759.5)Y + (1289.2 - 0)Z
VS/P = 3119.6X + 1473.2Y + 1289.2Z m/s
Equation (5.34),
VS/P = SQRT[ VS/PX2 + VS/PY2 + VS/PZ2 ]
VS/P = SQRT[ 3119.62 + 1473.22 + 1289.22 ]
VS/P = 3,683.0 m/s
V
V, and the zenith angle of the departure
asymptote. Injection occurs from an 200 km parking orbit. Earth's velocity
vector at departure is 25876.6X + 13759.5Y m/s.
SOLUTION,
Given: ro = (6,378.14 + 200) × 1,000 = 6,578,140 m
r = 0.473265X - 0.899215Y AU
VP = 25876.6X + 13759.5Y m/s
From problem 5.4,
VS = 28996.2X + 15232.7Y + 1289.2Z m/s
Equation (5.33),
VS/P = (VSX - VPX)X + (VSY - VPY)Y + (VSZ - VPZ)Z
VS/P = (28996.2 - 25876.6)X + (15232.7 - 13759.5)Y + (1289.2 - 0)Z
VS/P = 3119.6X + 1473.2Y + 1289.2Z m/s
Equation (5.34),
VS/P = SQRT[ VS/PX2 + VS/PY2 + VS/PZ2 ]
VS/P = SQRT[ 3119.62 + 1473.22 + 1289.22 ]
VS/P = 3,683.0 m/s
V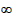 = VS/P = 3,683.0 m/s
Equations (5.35) and (5.36),
Vo = SQRT[ V
= VS/P = 3,683.0 m/s
Equations (5.35) and (5.36),
Vo = SQRT[ V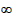 2 + 2 × GM / ro ]
Vo = SQRT[ 3,683.02 + 2 × 3.986005×1014 / 6,578,140 ]
Vo = 11,608.4 m/s
2 + 2 × GM / ro ]
Vo = SQRT[ 3,683.02 + 2 × 3.986005×1014 / 6,578,140 ]
Vo = 11,608.4 m/s
 V = Vo - SQRT[ GM / ro ]
V = Vo - SQRT[ GM / ro ]
 V = 11,608.4 - SQRT[ 3.986005×1014 / 6,578,140 ]
V = 11,608.4 - SQRT[ 3.986005×1014 / 6,578,140 ]
 V = 3,824.1 m/s
Equation (5.37),
r = SQRT[ 0.4732652 + (-0.899215)2 + 02 ]
r = 1.01615 AU
V = 3,824.1 m/s
Equation (5.37),
r = SQRT[ 0.4732652 + (-0.899215)2 + 02 ]
r = 1.01615 AU
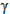 = arccos[(rX × vX + rY × vY + rZ × vZ) / (r × v)]
= arccos[(rX × vX + rY × vY + rZ × vZ) / (r × v)]
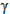 = arccos[ 0.473265 × 3119.6 - 0.899215 × 1473.2 + 0 × 1289.2) / (1.01615 × 3683.0)]
= arccos[ 0.473265 × 3119.6 - 0.899215 × 1473.2 + 0 × 1289.2) / (1.01615 × 3683.0)]
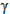 = 87.677o
= 87.677o
PROBLEM 5.7
For the spacecraft in Problems 5.3 and 5.4, given a miss distance of +18,500 km
at arrival, calculate the hyperbolic excess velocity, impact parameter, and
semi-major axis and eccentricity of the hyperbolic approach trajectory. Mars'
velocity vector at intercept is -23307.8X + 3112.0Y + 41.8Z m/s.
SOLUTION,
Given: d = 18,500 km / 149.597870×106 = 0.000123664 AU
r = 0.066842X + 1.561256Y + 0.030948Z AU
VP = -23307.8X + 3112.0Y + 41.8Z m/s
From Basics Constants,
GM of Mars = 4.282831×1013 m3/s2
From problem 5.4,
VS = -21147.0X + 3994.5Y - 663.3Z m/s
Equation (5.33),
VS/P = (VSX - VPX)X + (VSY - VPY)Y + (VSZ - VPZ)Z
VS/P = (-21147.0 + 23307.8)X + (3994.5 - 3112.0)Y + (-663.3 - 41.8)Z
VS/P = 2160.8X + 882.5Y - 705.1Z m/s
Equation (5.34),
VS/P = SQRT[ VS/PX2 + VS/PY2 + VS/PZ2 ]
VS/P = SQRT[ 2160.82 + 882.52 + (-705.1)2 ]
VS/P = 2,438.2 m/s
V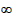 = VS/P = 2,438.2 m/s
Equations (5.38.A) and (5.38.B),
dx = -d × ry / SQRT[ rx2 + ry2 ]
dx = -0.000123664 × 1.561256 / SQRT[ 0.0668422 + 1.5612562 ]
dx = -0.000123551 AU
dy = d × rx / SQRT[ rx2 + ry2 ]
dy = 0.000123664 × 0.066842 / SQRT[ 0.0668422 + 1.5612562 ]
dy = 0.0000052896 AU
Equation (5.39),
= VS/P = 2,438.2 m/s
Equations (5.38.A) and (5.38.B),
dx = -d × ry / SQRT[ rx2 + ry2 ]
dx = -0.000123664 × 1.561256 / SQRT[ 0.0668422 + 1.5612562 ]
dx = -0.000123551 AU
dy = d × rx / SQRT[ rx2 + ry2 ]
dy = 0.000123664 × 0.066842 / SQRT[ 0.0668422 + 1.5612562 ]
dy = 0.0000052896 AU
Equation (5.39),
 = arccos[(dx × vx + dy × vy) / (d × v)]
= arccos[(dx × vx + dy × vy) / (d × v)]
 = arccos[(-0.000123551 × 2160.8 + 0.0000052896 × 882.5) / (0.000123664 × 2,438.2)]
= arccos[(-0.000123551 × 2160.8 + 0.0000052896 × 882.5) / (0.000123664 × 2,438.2)]
 = 150.451o
Equations (5.40) through (5.42),
b = d × sin
= 150.451o
Equations (5.40) through (5.42),
b = d × sin  b = 18,500 × sin(150.451)
b = 9,123.6 km
a = -GM / V
b = 18,500 × sin(150.451)
b = 9,123.6 km
a = -GM / V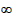 2
a = -4.282831×1013 / 2,438.22
a = -7.2043×106 m = -7,204.3 km
e = SQRT[ 1 + b2 / a2 ]
e = SQRT[ 1 + 9,123.62 / -7,204.32 ]
e = 1.6136
2
a = -4.282831×1013 / 2,438.22
a = -7.2043×106 m = -7,204.3 km
e = SQRT[ 1 + b2 / a2 ]
e = SQRT[ 1 + 9,123.62 / -7,204.32 ]
e = 1.6136
PROBLEM 5.8
As a spacecraft approaches Jupiter, it has a velocity of 9,470 m/s, a flight
path angle of 39.2 degrees, and a targeted miss distance of -2,500,000 km. At
intercept, Jupiter's velocity is 12,740 m/s with a flight path angle of 2.40
degrees. Calculate the spacecraft's velocity and flight path angle following
its swing-by of Jupiter.
Given: VP = 12,740 m/s
 P = 2.40o
VSi = 9,470 m/s
P = 2.40o
VSi = 9,470 m/s
 Si = 39.2o
d = -2,500,000 km
From Basics Constants,
GM of Jupiter = 1.26686×1017 m3/s2
Equations (5.44) and (5.45),
VP = (VP × cos
Si = 39.2o
d = -2,500,000 km
From Basics Constants,
GM of Jupiter = 1.26686×1017 m3/s2
Equations (5.44) and (5.45),
VP = (VP × cos  P)X + (VP × sin
P)X + (VP × sin  P)Y
VP = (12740 × cos(2.40))X + (12740 × sin(2.40))Y
VP = 12729X + 533Y m/s
VSi = (VSi × cos
P)Y
VP = (12740 × cos(2.40))X + (12740 × sin(2.40))Y
VP = 12729X + 533Y m/s
VSi = (VSi × cos  Si)X + (VSi × sin
Si)X + (VSi × sin  Si)Y
VSi = (9470 × cos(39.2))X + (9470 × sin(39.2))Y
VSi = 7339X + 5985Y m/s
Equations (5.46) and (5.47),
VS/Pi = ((VSi)X - VPX)X + ((VSi)Y - VPY)Y
VS/Pi = (7339 - 12729)X + (5985 - 533)Y
VS/Pi = -5390X + 5452Y m/s
VS/P = SQRT[ (VS/Pi)X2 + (VS/Pi)Y2 ]
VS/P = SQRT[ (-5390)2 + 54522 ]
VS/P = 7,667 m/s
V
Si)Y
VSi = (9470 × cos(39.2))X + (9470 × sin(39.2))Y
VSi = 7339X + 5985Y m/s
Equations (5.46) and (5.47),
VS/Pi = ((VSi)X - VPX)X + ((VSi)Y - VPY)Y
VS/Pi = (7339 - 12729)X + (5985 - 533)Y
VS/Pi = -5390X + 5452Y m/s
VS/P = SQRT[ (VS/Pi)X2 + (VS/Pi)Y2 ]
VS/P = SQRT[ (-5390)2 + 54522 ]
VS/P = 7,667 m/s
V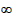 = VS/P = 7,667 m/s
Equation (5.48),
= VS/P = 7,667 m/s
Equation (5.48),
 i = arctan[ (VS/Pi)Y / (VS/Pi)X ]
i = arctan[ (VS/Pi)Y / (VS/Pi)X ]
 i = arctan[ 5452 / -5390 ]
i = arctan[ 5452 / -5390 ]
 i = 134.67o
Equations (5.40) through (5.42),
b = d × sin
i = 134.67o
Equations (5.40) through (5.42),
b = d × sin  b = -2,500,000 × sin(134.67)
b = -1,777,900 km
a = -GM / V
b = -2,500,000 × sin(134.67)
b = -1,777,900 km
a = -GM / V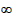 2
a = -1.26686×1017 / 76672
a = -2.1552×109 m = -2,155,200 km
e = SQRT[ 1 + b2 / a2 ]
e = SQRT[ 1 + (-1,777,900)2 / (-2,155,200)2 ]
e = 1.2963
Equation (5.49.B),
2
a = -1.26686×1017 / 76672
a = -2.1552×109 m = -2,155,200 km
e = SQRT[ 1 + b2 / a2 ]
e = SQRT[ 1 + (-1,777,900)2 / (-2,155,200)2 ]
e = 1.2963
Equation (5.49.B),
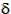 = -2 × arcsin( 1 / e )
= -2 × arcsin( 1 / e )
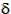 = -2 × arcsin( 1 / 1.2963 )
= -2 × arcsin( 1 / 1.2963 )
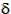 = -100.96o
Equation (5.50),
= -100.96o
Equation (5.50),
 f =
f =  i +
i + 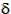
 f = 134.67 + (-100.96)
f = 134.67 + (-100.96)
 f = 33.71o
Equation (5.51),
VS/Pf = (VS/P × cos
f = 33.71o
Equation (5.51),
VS/Pf = (VS/P × cos  f)X + (VS/P × sin
f)X + (VS/P × sin  f)Y
VS/Pf = (7667 × cos(33.71))X + (7667 × sin(33.71))Y
VS/Pf = 6378X + 4255Y m/s
Equations (5.52) and (5.53),
VSf = ((VS/Pf)X + VPX)X + ((VS/Pf)Y + VPY)Y
VSf = (6378 + 12729)X + (4255 + 533)Y
VSf = 19107X + 4788Y m/s
VSf = SQRT[ (VSf)X2 + (VSf)Y2 ]
VSf = SQRT[ 191072 + 47882 ]
VSf = 19,698 m/s
Equation (5.54),
f)Y
VS/Pf = (7667 × cos(33.71))X + (7667 × sin(33.71))Y
VS/Pf = 6378X + 4255Y m/s
Equations (5.52) and (5.53),
VSf = ((VS/Pf)X + VPX)X + ((VS/Pf)Y + VPY)Y
VSf = (6378 + 12729)X + (4255 + 533)Y
VSf = 19107X + 4788Y m/s
VSf = SQRT[ (VSf)X2 + (VSf)Y2 ]
VSf = SQRT[ 191072 + 47882 ]
VSf = 19,698 m/s
Equation (5.54),
 Sf = arctan[ (VSf)Y / (VSf)X ]
Sf = arctan[ (VSf)Y / (VSf)X ]
 Sf = arctan[ 4788 / 19107 ]
Sf = arctan[ 4788 / 19107 ]
 Sf = 14.07o
Sf = 14.07o

V = Ve × LN[ M / (M - qt) ]
V = 3,100 × LN[ 30,000 / (30,000 - (30 × 60)) ]
V = 192 m/s
v of 700 m/s? SOLUTION, Given: Mf = 75,000 kg C = 3,100 m/s
V = 700 m/s Equation (1.20), Mo = Mf × e(DV / C) Mo = 75,000 × e(700 / 3,100) Mo = 94,000 kg Propellant mass, Mp = Mo - Mf Mp = 94,000 - 75,000 Mp = 19,000 kg
V = 12,000 - 7,790 = 4,210 m/s Equation (1.21), t = M / q × [ 1 - 1 / e(DV / C) ] t = 5,000 / 10 × [ 1 - 1 / e(4,210 / 3,000) ] t = 377 s
)1/2 = 47.3 cm
= 20o From Table 1, L* = 102-127 cm for LOX/RP-1, let's use 110 cm Equation (1.33), Vc = At × L* Vc = 1,756 × 110 = 193,160 cm3 From Figure 1.7, Lc = 66 cm (second-order approximation) Equation (1.35), Dc = SQRT[(Dt3 + 24/
× tan
× Vc) / (Dc + 6 × tan
× Lc)] Dc = SQRT[(47.33 + 24/
× tan(20) × 193,160) / (Dc + 6 × tan(20) × 66)] Dc = 56.6 cm (four interations)
p = 1.70 g/ml Ab =
× 1 × 10 = 31.416 m2 Equation (1.36), r = a × Pcn r = 5.5 × 5.00.4 = 10.47 mm/s Equation (1.37), q =
p × Ab × r q = 1.70 × 31.416 × 10.47 = 559 kg/s
AP = 1.95 g/ml
Al = 2.70 g/ml
HTPB = ≈0.93 g/ml Equation (1.38),
p = 1 /
i (w /
)i
p = 1 / [(0.68 / 1.95) + (0.18 / 2.70) + (0.14 / 0.93)]
p = 1.767
V. SOLUTION, Given: Mo1 = 120,000 + 9,000 + 30,000 + 3,000 + 3,000 = 165,000 kg Mf1 = 9,000 + 30,000 + 3,000 + 3,000 = 45,000 kg Isp1 = 260 s Mo2 = 30,000 + 3,000 + 3,000 = 36,000 kg Mf2 = 3,000 + 3,000 = 6,000 kg Isp2 = 320 s Equation (1.24), C1 = Isp1g C1 = 260 × 9.80665 = 2,550 m/s C2 = Isp2g C2 = 320 × 9.80665 = 3,138 m/s Equation (1.39),
V1 = C1 × LN[ Mo1 / Mf1 ]
V1 = 2,550 × LN[ 165,000 / 45,000 ]
V1 = 3,313 m/s
V2 = C2 × LN[ Mo2 / Mf2 ]
V2 = 3,138 × LN[ 36,000 / 6,000 ]
V2 = 5,623 m/s Equation (1.40),
VTotal =
V1 +
V2
VTotal = 3,313 + 5,623
VTotal = 8,936 m/s
2 × r3 / GM P = SQRT[ 4 ×
2 × r3 / GM ] P = SQRT[ 4 ×
2 × 6,578,1403 / 3.986005×1014 ] P = 5,310 s
2 × r3 / GM r = [ P2 × GM / (4 ×
2) ]1/3 r = [ 86,164.12 × 3.986005×1014 / (4 ×
2) ]1/3 r = 42,164,170 m
= 89o Equation (4.26), (Rp / r1)1,2 = ( -C ± SQRT[ C2 - 4 × (1 - C) × -sin2
]) / (2 × (1 - C)) where C = 2 × GM / (r1 × v12) C = 2 × 3.986005×1014 / (6,628,140 × 7,9002) C = 1.927179 (Rp / r1)1,2 = ( -1.927179 ± SQRT[ 1.9271792 - 4 × -0.927179 × -sin2(89) ]) / (2 × -0.927179) (Rp / r1)1,2 = 0.996019 and 1.082521 Perigee Radius, Rp = Rp1 = r1 × (Rp / r1)1 Rp = 6,628,140 × 0.996019 Rp = 6,601,750 m Altitude @ perigee = 6,601,750 / 1,000 - 6,378.14 = 223.6 km Apogee Radius, Ra = Rp2 = r1 × (Rp / r1)2 Ra = 6,628,140 × 1.082521 Ra = 7,175,100 m Altitude @ agogee = 7,175,100 / 1,000 - 6,378.14 = 797.0 km
= 89o Equation (4.27), e = SQRT[ (r1 × v12 / GM - 1)2 × sin2
+ cos2
] e = SQRT[ (6,628,140 × 7,9002 / 3.986005×1014 - 1)2 × sin2(89) + cos2(89) ] e = 0.0416170
from perigee point to launch point for the satellite in problem 4.8. SOLUTION, Given: r1 = 6,628,140 m v1 = 7,900 m/s
= 89o Equation (4.28), tan
= (r1 × v12 / GM) × sin
× cos
/ [(r1 × v12 / GM) × sin2
- 1] tan
= (6,628,140 × 7,9002 / 3.986005×1014) × sin(89) × cos(89) / [(6,628,140 × 7,9002 / 3.986005×1014) × sin2(89) - 1] tan
= 0.48329
= arctan(0.48329)
= 25.794o
= 86o
= 32o
2 = -60o From problem 4.10,
= 25.794o Equation (4.33), cos(i) = cos(
) × sin(
) cos(i) = cos(32) × sin(86) i = 32.223o Equations (4.34) and (4.36), tan(
) = tan(
) / cos(
) tan(
) = tan(32) / cos(86)
= 83.630o
=
-

= 83.630 - 25.794
= 57.836o Equations (4.35) and (4.37), tan(
) = sin(
) × tan(
) tan(
) = sin(32) × tan(86)
= 82.483o
1 =
2 -
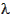
1 = -60 - 82.483
1 = -142.483o
= Sidereal time at -142.483 longitude, 2000-10-20, 15:00 UT
= 7h 27' 34" = 111.892o
O = 30 deg ×
/180 = 0.52360 radians
= 90 deg ×
/180 = 1.57080 radians Equation (4.40), cos E = (e + cos
) / (1 + e cos
) Eo = arccos[(0.1 + cos(0.52360)) / (1 + 0.1 × cos(0.52360))] Eo = 0.47557 radians E = arccos[(0.1 + cos(1.57080)) / (1 + 0.1 × cos(1.57080))] E = 1.47063 radians Equation (4.41), M = E - e × sin E Mo = 0.47557 - 0.1 × sin(0.47557) Mo = 0.42978 radians M = 1.47063 - 0.1 × sin(1.47063) M = 1.37113 radians Equation (4.39), n = SQRT[ GM / a3 ] n = SQRT[ 3.986005×1014 / 7,500,0003 ] n = 0.00097202 rad/s Equation (4.38), M - Mo = n × (t - tO) t = tO + (M - Mo) / n t = 0 + (1.37113 - 0.42978) / 0.00097202 t = 968.4 s
O = 90 ×
/180 = 1.57080 rad From problem 4.13, Mo = 1.37113 rad n = 0.00097202 rad/s Equation (4.38), M - Mo = n × (t - tO) M = Mo + n × (t - tO) M = 1.37113 + 0.00097202 × (1,200 - 0) M = 2.53755 METHOD #1, Low Accuracy: Equation (4.42),
~ M + 2 × e × sin M + 1.25 × e2 × sin 2M
~ 2.53755 + 2 × 0.1 × sin(2.53755) + 1.25 × 0.12 × sin(2 × 2.53755)
~ 2.63946 = 151.2 degrees METHOD #2, High Accuracy: Equation (4.41), M = E - e × sin E 2.53755 = E - 0.1 × sin E By iteration, E = 2.58996 radians Equation (4.40), cos E = (e + cos
) / (1 + e cos
) Rearranging variables gives, cos
= (cos E - e) / (1 - e cos E)
= arccos[(cos(2.58996) - 0.1) / (1 - 0.1 × cos(2.58996)]
= 2.64034 = 151.3 degrees
= 225 degrees Equations (4.43) and (4.44), r = a × (1 - e2) / (1 + e × cos
) r = 7,500,000 × (1 - 0.12) / (1 + 0.1 × cos(225)) r = 7,989,977 m
= arctan[ e × sin
/ (1 + e × cos
)]
= arctan[ 0.1 × sin(225) / (1 + 0.1 × cos(225))]
= -4.351 degrees Equation (4.45), v = SQRT[ GM × (2 / r - 1 / a)] v = SQRT[ 3.986005×1014 × (2 / 7,989,977 - 1 / 7,500,000)] v = 6,828 m/s
Moon = -0.00338 × cos(i) / n
Moon = -0.00338 × cos(51.6) / 15.5
Moon = -0.000135 deg/day
Sun = -0.00154 × cos(i) / n
Sun = -0.00154 × cos(51.6) / 15.5
Sun = -0.0000617 deg/day
Moon = 0.00169 × (4 - 5 × sin2 i) / n
Moon = 0.00169 × (4 - 5 × sin2 51.6) / 15.5
Moon = 0.000101 deg/day
Sun = 0.00077 × (4 - 5 × sin2 i) / n
Sun = 0.00077 × (4 - 5 × sin2 51.6) / 15.5
Sun = 0.000046 deg/day
J2 = -2.06474×1014 × a-7/2 × (cos i) × (1 - e2)-2
J2 = -2.06474×1014 × (7,500)-7/2 × (cos 28.5) × (1 - (0.1)2)-2
J2 = -5.067 deg/day
J2 = 1.03237×1014 × a-7/2 × (4 - 5 × sin2 i) × (1 - e2)-2
J2 = 1.03237×1014 × (7,500)-7/2 × (4 - 5 × sin2 28.5) × (1 - (0.1)2)-2
J2 = 8.250 deg/day
= 2.62×10-12 kg/m3 H = 58.2 km Equation (4.6), V = SQRT[ GM / a ] V = SQRT[ 3.986005×1014 / 6,778,140 ] V = 7,669 m/s Equations (4.53) through (4.55),
arev = (-2 ×
× CD × A ×
× a2) / m
arev = (-2 ×
× 2.67 × 8 × 2.62×10-12 × 6,778,1402) / 1,000
arev = -16.2 m
Prev = (-6 ×
2 × CD × A ×
× a2) / (m × V)
Prev = (-6 ×
2 × 2.67 × 8 × 2.62×10-12 × 6,778,1402) / (1,000 × 7,669)
Prev = -0.0199 s
Vrev = (
× CD × A ×
× a × V) / m
Vrev = (
× 2.67 × 8 × 2.62×10-12 × 6,778,140 × 7,669) / 1,000
Vrev = 0.00914 m/s Equation (4.56), L ~ -H /
arev L ~ -(58.2 × 1,000) / -16.2 L ~ 3,600 revolutions
VA = VtxA - ViA
VA = 10,239 - 7,784
VA = 2,455 m/s
VB = VfB - VtxB
VB = 3,075 - 1,597
VB = 1,478 m/s
VT =
VA +
VB
VT = 2,455 + 1,478
VT = 3,933 m/s
= arccos[(atx × (1 - e2) / rB - 1) / e ]
= arccos[(30,000,000 × (1 - 0.7807292) / 42,164,170 - 1) / 0.780729 ]
= 157.670 degrees
= arctan[ e × sin
/ (1 + e × cos
)]
= arctan[ 0.780729 × sin(157.670) / (1 + 0.780729 × cos(157.670))]
= 46.876 degrees Equations (4.59) through (4.63), ViA = SQRT[ GM / rA ] ViA = SQRT[ 3.986005×1014 / 6,578,140 ] ViA = 7,784 m/s VfB = SQRT[ GM / rB ] VfB = SQRT[ 3.986005×1014 / 42,164,170 ] VfB = 3,075 m/s VtxA = SQRT[ GM × (2 / rA - 1 / atx)] VtxA = SQRT[ 3.986005×1014 × (2 / 6,578,140 - 1 / 30,000,000)] VtxA = 10,388 m/s VtxB = SQRT[ GM × (2 / rB - 1 / atx)] VtxB = SQRT[ 3.986005×1014 × (2 / 42,164,170 - 1 / 30,000,000)] VtxB = 2,371 m/s
VA = VtxA - ViA
VA = 10,388 - 7,784
VA = 2,604 m/s Equation (4.69),
VB = SQRT[ VtxB2 + VfB2 - 2 × VtxB × VfB × cos
]
VB = SQRT[ 2,3712 + 3,0752 - 2 × 2,371 × 3,075 × cos(46.876)]
VB = 2,260 m/s Equation (4.65),
VT =
VA +
VB
VT = 2,604 + 2,260
VT = 4,864 m/s Equations (4.70) and (4.71), E = arccos[(e + cos
) / (1 + e cos
)] E = arccos[(0.780729 + cos(157.670)) / (1 + 0.780729 × cos(157.670))] E = 2.11688 radians TOF = (E - e × sin E) × SQRT[ atx3 / GM ] TOF = (2.11688 - 0.780729 × sin(2.11688)) × SQRT[ 30,000,0003 / 3.986005×1014 ] TOF = 11,931 s = 3.314 hours
= 28 - 20 = 8 degrees Equation (4.6), Vi = SQRT[ GM / r ] Vi = SQRT[ 3.986005×1014 / 6,978,140 ] Vi = 7,558 m/s Equation (4.73),
V = 2 × Vi × sin(
/2)
V = 2 × 7,558 × sin(8/2)
V = 1,054 m/s
= 28 degrees From problem 4.19, VfB = 3,075 m/s VtxB = 1,597 m/s
VA = 2,455 m/s Equation (4.74),
VB = SQRT[ VtxB2 + VfB2 - 2 × VtxB × VfB × cos
]
VB = SQRT[ 1,5972 + 3,0752 - 2 × 1,597 × 3,075 × cos(28)]
VB = 1,826 m/s Equation (4.65),
VT =
VA +
VB
VT = 2,455 + 1,826
VT = 4,281 m/s
i = 75 degrees if = 32 degrees
f = 80 degrees Equation (4.75), a1 = sin(ii)cos(
i) = sin(30)cos(75) = 0.129410 a2 = sin(ii)sin(
i) = sin(30)sin(75) = 0.482963 a3 = cos(ii) = cos(30) = 0.866025 b1 = sin(if)cos(
f) = sin(32)cos(80) = 0.0920195 b2 = sin(if)sin(
f) = sin(32)sin(80) = 0.521869 b3 = cos(if) = cos(32) = 0.848048
= arccos(a1 × b1 + a2 × b2 + a3 × b3)
= arccos(0.129410 × 0.0920195 + 0.482963 × 0.521869 + 0.866025 × 0.848048)
= 3.259 degrees
, true anomaly, impact parameter, periapsis radius, and parameter p. SOLUTION, From Basics Constants, GM of Mars = 4.282831×1013 m3/s2 Given: r = 100,000 × 1,000 = 100,000,000 m v = 5,140.0 m/s
= -85.300o Equations (4.30) and (4.32), e = SQRT[ (r × v2 / GM - 1)2 × cos2
+ sin2
] e = SQRT[ (100,000,000 × 5,1402 / 4.282831×1013 - 1)2 × cos2(-85.3) + sin2(-85.3) ] e = 5.0715 a = 1 / ( 2 / r - v2 / GM ) a = 1 / ( 2 / 100,000,000 - 5,1402 / 4.282831×1013 ) a = -1,675,400 m Equations (4.80) through (4.85), sin(
/2) = 1 / e
= 2 × arcsin( 1 / 5.0715 )
= 22.744o cos
= -1 / e
= arccos( -1 / 5.0715 )
= 101.37o
= arccos[ (a × (1 - e2) - r) / (e × r) ]
= arccos[ (-1,675,400 × (1 - 5.07152) - 100,000,000) / (5.0715 × 100,000,000) ]
= -96.633o b = -a / tan(
/2) b = 1,675.4 / tan(22.744/2) b = 8,330.0 km ro = a × (1 - e) ro = -1,675.4 × (1 - 5.0715) ro = 6,821.4 km p = a × (1 - e2) p = -1,675.4 × (1 - 5.07152) p = 41,416 km
= 75o Equations (4.43) through (4.45), r = a × (1 - e2) / (1 + e × cos
) r = -1,675,400 × (1 - 5.07152) / (1 + 5.0715 × cos(75)) r = 17,909,000 m
= arctan[ e × sin
/ (1 + e × cos
)]
= arctan[ 5.0715 × sin(75) / (1 + 5.0715 × cos(75))]
= 64.729o v = SQRT[ GM × (2 / r - 1 / a)] v = SQRT[ 4.282831×1013 × (2 / 17,909,000 - 1 / -1,675,400)] v = 5,508.7 m/s
O = 15o
= 120o Equation (4.87), cosh F = (e + cos
) / (1 + e cos
) Fo = arccosh[(1.1823 + cos(15)) / (1 + 1.1823 × cos(15))] Fo = 0.07614 F = arccosh[(1.1823 + cos(120)) / (1 + 1.1823 × cos(120))] F = 1.10023 Equation (4.86), t - tO = SQRT[(-a)3 / GM ] × [(e × sinh F - F) - (e × sinh Fo - Fo)] t - tO = SQRT[(36,000,000)3 / 3.986005×1014 ] × [(1.1823 × sinh(1.10023) - 1.10023) - (1.1823 × sinh(0.07614) - 0.07614)] t - tO = 5,035 s = 1.399 hours
2 = Vbo2 - Vesc2 V
= SQRT[ 11,5002 - 11,0092 ] V
= 3,325 m/s
= arccos[(atx × (1 - e2) / rB - 1) / e ]
= arccos[(1.3 × (1 - 0.2307692) / 1.524 - 1) / 0.230769 ]
= 146.488 degrees Equations (4.70) and (4.71), E = arccos[(e + cos
) / (1 + e cos
)] E = arccos[(0.230769 + cos(146.488)) / (1 + 0.230769 × cos(146.488))] E = 2.41383 radians TOF = (E - e × sin E) × SQRT[ atx3 / GM ] TOF = (2.41383 - 0.230769 × sin(2.41383)) × SQRT[ (194.48×109)3 / 1.327124×1020 ] TOF = 16,827,800 s = 194.77 days
2-
1 = 146.488o t2-t1 = 194.77 days
t = 0.5240o/day Equation (5.1),
= (
2-
1) -
t × (t2-t1)
= 146.488 - 0.5240 × 194.77
= 44.43o
= arccos[ (0.473265 × 0.066842 - 0.899215 × 1.561256) / (1.016153 × 1.562993) ]
= 149.770967o Equations (5.9), (5.10) and (5.11), k = r1 × r2 × (1 - cos
) k = 1.016153 × 1.562993 × (1 - cos(149.770967)) k = 2.960511 AU
= r1 + r2
= 1.016153 + 1.562993
= 2.579146 AU m = r1 × r2 × (1 + cos
) m = 1.016153 × 1.562993 × (1 + cos(149.770967)) m = 0.215969 AU Equations (5.18) and (5.19), pi = k / (
+ SQRT(2 × m)) pi = 2.960511 / (2.579146 + SQRT(2 × 0.215969)) pi = 0.914764 AU pii = k / (
- SQRT(2 × m)) pii = 2.960511 / (2.579146 - SQRT(2 × 0.215969)) pii = 1.540388 AU Since
<
, 0.914764 < p <
Equation (5.12), Select trial value, p = 1.2 AU a = m × k × p / [(2 × m -
2) × p2 + 2 × k ×
× p - k2] a = 0.215969 × 2.960511 × 1.2 / [(2 × 0.215969 - 2.5791462) × 1.22 + 2 × 2.960511 × 2.579146 × 1.2 - 2.9605112] a = 1.270478 AU Equations (5.5), (5.6) and (5.7), f = 1 - r2 / p × (1 - cos
) f = 1 - 1.562993 / 1.2 × (1 - cos(149.770967)) f = -1.427875 g = r1 × r2 × sin
/ SQRT[ GM × p ] g = 1.016153 × 1.562993 × sin(149.770967) / SQRT[ 3.964016×10-14 × 1.2 ] g = 3,666,240
= SQRT[ GM / p ] × tan(
/2) × [(1 - cos
) / p - 1/r1 - 1/r2 ]
= SQRT[ 3.964016×10-14 / 1.2 ] × tan(149.770967/2) × [(1 - cos(149.770967)) / 1.2 - 1/1.016153 - 1/1.562993 ]
= -4.747601×10-8 Equation (5.13),
E = arccos[ 1 - r1 / a × (1 - f) ]
E = arccos[ 1 - 1.016153 / 1.270478 × (1 + 1.427875) ]
E = 2.798925 radians Equation (5.16), t = g + SQRT[ a3 / GM ] × (
E - sin
E) t = 3,666,240 + SQRT[ 1.2704783 / 3.964016×10-14 ] × (2.798925 - sin(2.798925)) t = 21,380,951 s = 247.4647 days Select new trial value of p and repeat above steps, p = 1.300000 AU, a = 1.443005 AU, t = 178.9588 days Equation (5.20), pn+1 = pn + (t - tn) × (pn - pn-1) / (tn - tn-1) pn+1 = 1.3 + (207 - 178.9588) × (1.3 - 1.2) / (178.9588 - 247.4647) pn+1 = 1.259067 AU Recalculate using new value of p, p = 1.259067 AU, a = 1.336197 AU, t = 201.5624 days Perform additional iterations, p = 1.249221 AU, a = 1.318624 AU, t = 207.9408 days p = 1.250673 AU, a = 1.321039 AU, t = 206.9733 days p = 1.250633 AU, a = 1.320971 AU, t = 206.9999 days <-- close enough
= 149.770967o Equations (5.5), (5.6) and (5.7), f = 1 - r2 / p × (1 - cos
) f = 1 - 1.562993 / 1.250633 × (1 - cos(149.770967)) f = -1.329580 g = r1 × r2 × sin
/ SQRT[ GM × p ] g = 1.016153 × 1.562993 × sin(149.770967) / SQRT[ 3.964016×10-14 × 1.250633 ] g = 3,591,258
= SQRT[ GM / p ] × tan(
/2) × [(1 - cos
) / p - 1/r1 - 1/r2 ]
= SQRT[ 3.964016×10-14 / 1.250633 ] × tan(149.770967/2) × [(1 - cos(149.770967)) / 1.250633 - 1/1.016153 - 1/1.562993 ]
= -8.795872×10-8
= 1 - r1 / p × (1 - cos
)
= 1 - 1.016153 / 1.250633 × (1 - cos(149.770967))
= -0.514536 Equation (5.3), v1 = (r2 - f × r1) / g v1 = [(0.066842 + 1.329580 × 0.473265) / 3,591,258] X + [(1.561256 + 1.329580 × -0.899215) / 3,591,258] Y + [(0.030948 + 1.329580 × 0) / 3,591,258] Z v1 = 0.000000193828X + 0.000000101824Y + 0.00000000861759Z AU/s × 149.597870×109 v1 = 28996.2X + 15232.7Y + 1289.2Z m/s Equation (5.4), v2 =
× r1 +
× v1 v2 = [-8.795872×10-8 × 0.473265 - 0.514536 × 0.000000193828] X + [-8.795872×10-8 × -0.899215 - 0.514536 × 0.000000101824] Y + [-8.795872×10-8 × 0 - 0.514536 × 0.00000000861759] Z v2 = -0.000000141359X + 0.0000000267017Y - 0.00000000443406Z AU/s × 149.597870×109 v2 = -21147.0X + 3994.5Y - 663.3Z m/s
= nX / n cos
= 9.12746×1013 / 1.95977×1014
= 297.76o cos
= n • e / (n × e) cos
= (9.12746×1013 × 0.106639 - 1.73424×1014 × (-0.204632) + 0 × (-0.000037)) / (1.95977×1014 × 0.230751)
= 359.77o cos
o = e • r / (e × r) cos
o = (0.106639 × 7.079944×1010 - 0.204632 × (-1.345206×1011) - 0.000037 × 0) / (0.230751 × 1.520144×1011)
o = 0.226o cos uo = n • r / (n × r) uo = 0 (launch point = ascending node) Equations (5.31) and (5.32),
=
+
= 297.76 + 359.77
= 297.53o
o =
+
+
o
o = 297.76 + 359.77 + 0.23
o = 297.76o
V, and the zenith angle of the departure asymptote. Injection occurs from an 200 km parking orbit. Earth's velocity vector at departure is 25876.6X + 13759.5Y m/s. SOLUTION, Given: ro = (6,378.14 + 200) × 1,000 = 6,578,140 m r = 0.473265X - 0.899215Y AU VP = 25876.6X + 13759.5Y m/s From problem 5.4, VS = 28996.2X + 15232.7Y + 1289.2Z m/s Equation (5.33), VS/P = (VSX - VPX)X + (VSY - VPY)Y + (VSZ - VPZ)Z VS/P = (28996.2 - 25876.6)X + (15232.7 - 13759.5)Y + (1289.2 - 0)Z VS/P = 3119.6X + 1473.2Y + 1289.2Z m/s Equation (5.34), VS/P = SQRT[ VS/PX2 + VS/PY2 + VS/PZ2 ] VS/P = SQRT[ 3119.62 + 1473.22 + 1289.22 ] VS/P = 3,683.0 m/s V
= VS/P = 3,683.0 m/s Equations (5.35) and (5.36), Vo = SQRT[ V
2 + 2 × GM / ro ] Vo = SQRT[ 3,683.02 + 2 × 3.986005×1014 / 6,578,140 ] Vo = 11,608.4 m/s
V = Vo - SQRT[ GM / ro ]
V = 11,608.4 - SQRT[ 3.986005×1014 / 6,578,140 ]
V = 3,824.1 m/s Equation (5.37), r = SQRT[ 0.4732652 + (-0.899215)2 + 02 ] r = 1.01615 AU
= arccos[(rX × vX + rY × vY + rZ × vZ) / (r × v)]
= arccos[ 0.473265 × 3119.6 - 0.899215 × 1473.2 + 0 × 1289.2) / (1.01615 × 3683.0)]
= 87.677o
= VS/P = 2,438.2 m/s Equations (5.38.A) and (5.38.B), dx = -d × ry / SQRT[ rx2 + ry2 ] dx = -0.000123664 × 1.561256 / SQRT[ 0.0668422 + 1.5612562 ] dx = -0.000123551 AU dy = d × rx / SQRT[ rx2 + ry2 ] dy = 0.000123664 × 0.066842 / SQRT[ 0.0668422 + 1.5612562 ] dy = 0.0000052896 AU Equation (5.39),
= arccos[(dx × vx + dy × vy) / (d × v)]
= arccos[(-0.000123551 × 2160.8 + 0.0000052896 × 882.5) / (0.000123664 × 2,438.2)]
= 150.451o Equations (5.40) through (5.42), b = d × sin
b = 18,500 × sin(150.451) b = 9,123.6 km a = -GM / V
2 a = -4.282831×1013 / 2,438.22 a = -7.2043×106 m = -7,204.3 km e = SQRT[ 1 + b2 / a2 ] e = SQRT[ 1 + 9,123.62 / -7,204.32 ] e = 1.6136
P = 2.40o VSi = 9,470 m/s
Si = 39.2o d = -2,500,000 km From Basics Constants, GM of Jupiter = 1.26686×1017 m3/s2 Equations (5.44) and (5.45), VP = (VP × cos
P)X + (VP × sin
P)Y VP = (12740 × cos(2.40))X + (12740 × sin(2.40))Y VP = 12729X + 533Y m/s VSi = (VSi × cos
Si)X + (VSi × sin
Si)Y VSi = (9470 × cos(39.2))X + (9470 × sin(39.2))Y VSi = 7339X + 5985Y m/s Equations (5.46) and (5.47), VS/Pi = ((VSi)X - VPX)X + ((VSi)Y - VPY)Y VS/Pi = (7339 - 12729)X + (5985 - 533)Y VS/Pi = -5390X + 5452Y m/s VS/P = SQRT[ (VS/Pi)X2 + (VS/Pi)Y2 ] VS/P = SQRT[ (-5390)2 + 54522 ] VS/P = 7,667 m/s V
= VS/P = 7,667 m/s Equation (5.48),
i = arctan[ (VS/Pi)Y / (VS/Pi)X ]
i = arctan[ 5452 / -5390 ]
i = 134.67o Equations (5.40) through (5.42), b = d × sin
b = -2,500,000 × sin(134.67) b = -1,777,900 km a = -GM / V
2 a = -1.26686×1017 / 76672 a = -2.1552×109 m = -2,155,200 km e = SQRT[ 1 + b2 / a2 ] e = SQRT[ 1 + (-1,777,900)2 / (-2,155,200)2 ] e = 1.2963 Equation (5.49.B),
= -2 × arcsin( 1 / e )
= -2 × arcsin( 1 / 1.2963 )
= -100.96o Equation (5.50),
f =
i +
f = 134.67 + (-100.96)
f = 33.71o Equation (5.51), VS/Pf = (VS/P × cos
f)X + (VS/P × sin
f)Y VS/Pf = (7667 × cos(33.71))X + (7667 × sin(33.71))Y VS/Pf = 6378X + 4255Y m/s Equations (5.52) and (5.53), VSf = ((VS/Pf)X + VPX)X + ((VS/Pf)Y + VPY)Y VSf = (6378 + 12729)X + (4255 + 533)Y VSf = 19107X + 4788Y m/s VSf = SQRT[ (VSf)X2 + (VSf)Y2 ] VSf = SQRT[ 191072 + 47882 ] VSf = 19,698 m/s Equation (5.54),
Sf = arctan[ (VSf)Y / (VSf)X ]
Sf = arctan[ 4788 / 19107 ]
Sf = 14.07o




















